2011全国硕士研究生招生考试《数学1》真题
- 推荐等级:
- 发布时间:2021-12-30 13:51
- 卷面总分:20分
- 答题时间:240分钟
- 试卷题量:20题
- 练习次数:2次
- 试卷分类:数学一
- 试卷类型:历年真题
试卷预览
设随机变量X与Y相互独立,且EX与EY存在,记U=max{X,Y},V=min{X,Y},则E(UV)=
- 查看答案开始考试
正确答案:B
本题解析:
本题考查相互独立的两个随机变量简单函数的数字特征,显然当X与Y相互独立时E(X·Y)=EX·EY.我们有公式对解题也是有用的
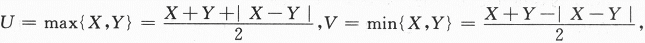 .
.(方法一)
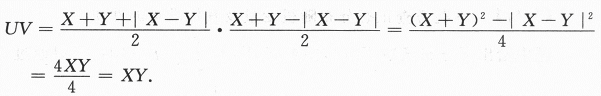
故E(UV)=E(X·Y)=EX·EY,答案应选(B).(方法二)UV=max{X,Y)·min{X,Y)=XY,因为二个中大的一个乘小的一个就等于这两个相乘.E(U·V)=E(X·Y)=EX·EY,答案应选(B)
曲线y=(x-1)(x-2)^2(x-3)^3(x-4)^4的拐点是
- 查看答案开始考试
正确答案:C
本题解析:
(方法一)图示法:由曲线方程y=(x-1)(x-2)^2(x-3)^3(x-4)^4可知,该曲线和x轴有四个交点,即x=1,x=2,x=3,x=4,且在x=2取极大值,x=4取极小值,则拐点只能在另外两个点上,由下图不难看出(3,0)为拐点,故应选(C).
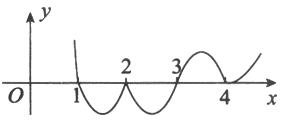
(方法二)记g(x)=(x-1)(x-2)^2(x-4)^4,则y-(x-3)^3g(x)
设g(x)在x=3处的泰勒展开式为g(x)=a0+a1(x-3)+…
则y=a0(x-3)^3+a0(x-3)^4+…
由该式可知y"(3)=0,y'"(3)=a0·3!≠0
因为a0=g(3)≠0.由拐点的第二充分条件知,(3,0)为拐点
其他考生还关注了更多 +
- 全国硕士研究生入学考试《数学2》模拟试卷7
试卷分类:数学二
练习次数:0次
- 全国硕士研究生入学考试《数学2》模拟试卷6
试卷分类:数学二
练习次数:0次
- 全国硕士研究生入学考试《数学2》模拟试卷5
试卷分类:数学二
练习次数:0次
- 全国硕士研究生入学考试《数学2》模拟试卷4
试卷分类:数学二
练习次数:0次
- 全国硕士研究生入学考试《数学2》模拟试卷3
试卷分类:数学二
练习次数:0次
- 全国硕士研究生入学考试《数学2》模拟试卷2
试卷分类:数学二
练习次数:0次
- 全国硕士研究生入学考试《数学2》模拟试卷1
试卷分类:数学二
练习次数:0次
- 2012全国硕士研究生入学考试《数学2》真题
试卷分类:数学二
练习次数:0次
- 2011全国硕士研究生入学考试《数学2》真题
试卷分类:数学二
练习次数:0次
- 2010全国硕士研究生入学考试《数学2》真题
试卷分类:数学二
练习次数:0次




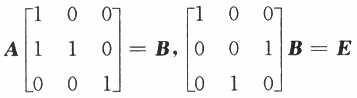 即AP1-B,P2B=E故
即AP1-B,P2B=E故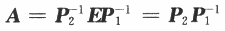 即应选(D)
即应选(D)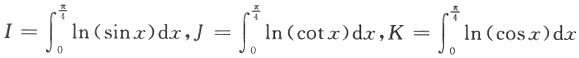 ,则I,J,K的大小关系为
,则I,J,K的大小关系为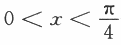 时,0
时,0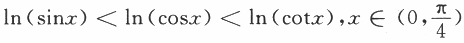
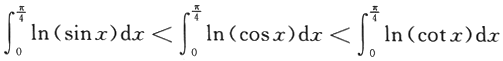 ,即I
,即I
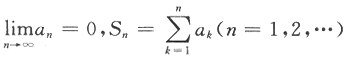 无界,则幂级数
无界,则幂级数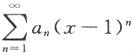 的收敛域为
的收敛域为