2008全国硕士研究生招生考试《数学1》真题
- 推荐等级:
- 发布时间:2021-12-30 13:50
- 卷面总分:23分
- 答题时间:240分钟
- 试卷题量:23题
- 练习次数:3次
- 试卷分类:数学一
- 试卷类型:历年真题
试卷预览
设随机变量X~N(0,1),Y~N(1,4),且相关系数ρXY=1,则
- 查看答案开始考试
正确答案:D
本题解析:
由相关系数的性质可知:如果|ρXY|=1,则必有P{Y=aX+b}=1,(a≠0),现在题设条件ρXY=1,只要在P{Y=±2X±1}=1四个选项中选一就可以了,实际上只要确定它们的正负号即可,本题可以从X~N(0,1)和Y~N(1,4)及ρXY=1直接推出P{Y=aX+b}=1中的a,b值.但更方便的,不如直接定出a,b的正负号更简单.
【求解】先来确定常数b,由P{Y=aX+b}=1.可得到E(Y)=aE(X)+b再因为X~N(0,1),Y~N(1,4),所以,1=a?0+b,即得b=1现来求常数a,实际上只要判定a的正负号就可以了.
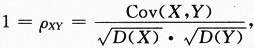
而Cov(X,Y)=Cov(X,aX+b)=aCov(X,X)=a故a>0.答案应选(D).
【评注】从
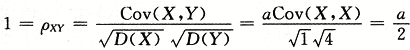 ,也可得到a=2
,也可得到a=2
设随机变量X,Y独立同分布,且X的分布函数为F(x),则Z=max{X,Y}的分布函数为
- 查看答案开始考试
正确答案:A
本题解析:
随机变量Z=max(X,Y)的分布函数Fz(x)应为Fz(x)=P{Z≤x},由此定义不难推出Fz(x).【求解】
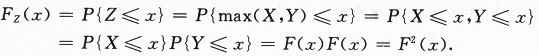 故答案应选(A).
故答案应选(A).【评注】不难验证(B)F(x)F(y)恰是二维随机变量(X,Y)的分布函数.(C)1-[1-F(x)]^2则是随机变量min(X,Y)的分布函数.(D)[1-F(x)][1-F(y)]本身不是分布函数,因它不满足分布函数的充要条件.
设A为三阶实对称矩阵,如果二次曲面方程
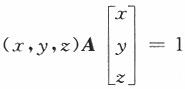
在正交变换下的标准方程的图形如图所示,
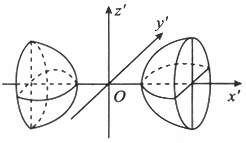
则A的正特征值的个数为
- 查看答案开始考试
正确答案:B
本题解析:
本题把线性代数与解析几何的内容有机的联系起来,首先要明白所给图形是什么曲面?其标准方程是什么? 双叶双曲面,标准方程是:
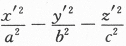 =1其次,二次型经正交变换化为标准形时,其平方项的系数就是A的特征值,所以应选(B).
=1其次,二次型经正交变换化为标准形时,其平方项的系数就是A的特征值,所以应选(B).很多考生选择(C),是不是把标准方程记成了图1} 而忽略了本题的条件是x^TAx=1.
设A为n阶非零矩阵,E为n阶单位矩阵,若A^3=O,则
- 查看答案开始考试
正确答案:C
本题解析:
判断矩阵A可逆通常用定义,或者用充要条件行列式|A|≠0(当然|A|≠0又有很多等价的说法).因为(E-A)(E+A+A^2)=E-A^3=E,(E+A)(E-A+A^2)=E+A^3=E,所以,由定义知E-A,E+A均可逆.故选(C).
【评注】本题用特征值也是简捷的,由A^3=O
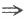 A的特征值λ=0
A的特征值λ=0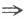 E-A(或E+A)特征值均不为0
E-A(或E+A)特征值均不为0 |E-A|≠0(或|E+A|≠0)
|E-A|≠0(或|E+A|≠0) E-A(或E+A)可逆
E-A(或E+A)可逆
设函数f(x)在(-∞,+∞)内单调有界,{xn}为数列,下列命题正确的是
- 查看答案开始考试
正确答案:B
本题解析:
(方法一)由于{xn}单调,f(xn)单调有界,则数列{f(xn)}单调有界.由单调有界准则知数列{f(xn)}收敛,故应选(B). (方法二)排除法:若取
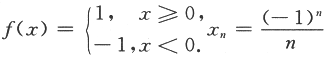 ,则显然f(xn)单调,{x}收敛,但
,则显然f(xn)单调,{x}收敛,但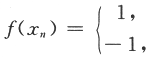 显然{f(xn)}不收敛,这样就排除了(A).若取f(xn)=arctanx,x=n,则f(xn)=arctann,显然{f(xn)}收敛且单调,但{xn}不收敛,这样就排除了(C)和(D),故应选(B)
显然{f(xn)}不收敛,这样就排除了(A).若取f(xn)=arctanx,x=n,则f(xn)=arctann,显然{f(xn)}收敛且单调,但{xn}不收敛,这样就排除了(C)和(D),故应选(B)
其他考生还关注了更多 +
- 全国硕士研究生入学考试《数学2》模拟试卷7
试卷分类:数学二
练习次数:0次
- 全国硕士研究生入学考试《数学2》模拟试卷6
试卷分类:数学二
练习次数:0次
- 全国硕士研究生入学考试《数学2》模拟试卷5
试卷分类:数学二
练习次数:0次
- 全国硕士研究生入学考试《数学2》模拟试卷4
试卷分类:数学二
练习次数:0次
- 全国硕士研究生入学考试《数学2》模拟试卷3
试卷分类:数学二
练习次数:0次
- 全国硕士研究生入学考试《数学2》模拟试卷2
试卷分类:数学二
练习次数:0次
- 全国硕士研究生入学考试《数学2》模拟试卷1
试卷分类:数学二
练习次数:0次
- 2012全国硕士研究生入学考试《数学2》真题
试卷分类:数学二
练习次数:0次
- 2011全国硕士研究生入学考试《数学2》真题
试卷分类:数学二
练习次数:0次
- 2010全国硕士研究生入学考试《数学2》真题
试卷分类:数学二
练习次数:0次

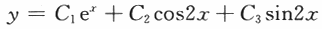 可知其特征根为.
可知其特征根为.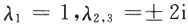
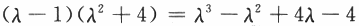 ,
,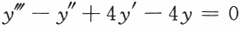 ,应选(D).
,应选(D).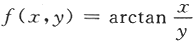 在点(0,1)处的梯度等于
在点(0,1)处的梯度等于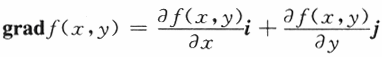 因为,
因为,
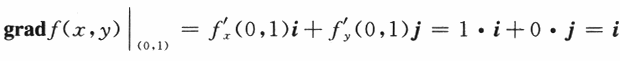
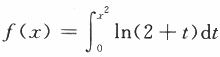 ,则f’(x)的零点个数为
,则f’(x)的零点个数为