2020年全国硕士研究生入学考试《数学三》真题
- 推荐等级:
- 发布时间:2021-12-24 09:57
- 卷面总分:23分
- 答题时间:240分钟
- 试卷题量:23题
- 练习次数:3次
- 试卷分类:数学三
- 试卷类型:历年真题
试卷预览
设A,B,C为三个随机事件,且P(A)=P(B)=P(C)=1/4,P(AB)=0,P(AC)=P(BC)=1/12,则A,B,C恰有一个事件发生的概率为( )
- 查看答案开始考试
正确答案:D
本题解析:

设A为3阶矩阵,a1,a2为A的属于特征值1的线性无关的特征向量,a3为A的属于特征值-1的特征向量,则满足
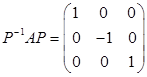 得可逆矩阵P为( )
得可逆矩阵P为( )- 查看答案开始考试
正确答案:D
本题解析:
a1,a2是A属于特征值1的线性无关的特征向量,即Aa1=a1,Aa2=a2,故A(a1+a2)=a1+a2,即a1+a2也是A属于特征值1的特征向量。
设k1(a1+a2)+k2a2=0,即k1a1+(k1+k2)a2=0,
由于a1,a2线性无关,故k1=k2=0,即a1+a2,a2线性无关。
a3是A属于特征值-1的特征向量,即Aa3=-a3,因此A(-a3)=-(-a3),即-a3也是A属于特征值-1的特征向量
可取P=(a1+a2,-a3,a2),则P是可逆矩阵,且满足。
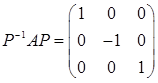
故应选D项。
设4阶矩阵A=(aij)不可逆,元素a12对应的代数余子式A12≠0,a1,a2,a3,a4为矩阵A的列向量组,A*为A的伴随矩阵,则A*x=0的通解为( )
- 查看答案开始考试
正确答案:C
本题解析:
由A不可逆知,r(A)<4,又元素a12对应的代数余子式A12≠0,故r(A)≥3,从而r(A)=3。
由
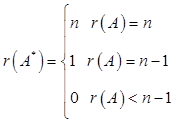 ,可知r(A*)=1。
,可知r(A*)=1。故A*x=0的基础解系含有3个解向量。
因a1,a2,a3,a4为矩阵A的列向量组,则a1,a3,a4可看做作A12对应矩阵列向量组的延长组,故a1,a3,a4线性无关。
又A*A=A*(a1,a2,a3,a4)=|A|E=0,故a1,a3,a4均为A*x=0的解。
综上,a1,a3,a4为A*x=0的一个基础解系,故A*x=0得通解为x=k1a1+k2a3+k3a4,其中k1,k2,k3为任意常数。
其他考生还关注了更多 +
- 全国硕士研究生入学考试《数学2》模拟试卷7
试卷分类:数学二
练习次数:0次
- 全国硕士研究生入学考试《数学2》模拟试卷6
试卷分类:数学二
练习次数:0次
- 全国硕士研究生入学考试《数学2》模拟试卷5
试卷分类:数学二
练习次数:0次
- 全国硕士研究生入学考试《数学2》模拟试卷4
试卷分类:数学二
练习次数:0次
- 全国硕士研究生入学考试《数学2》模拟试卷3
试卷分类:数学二
练习次数:0次
- 全国硕士研究生入学考试《数学2》模拟试卷2
试卷分类:数学二
练习次数:0次
- 全国硕士研究生入学考试《数学2》模拟试卷1
试卷分类:数学二
练习次数:0次
- 2012全国硕士研究生入学考试《数学2》真题
试卷分类:数学二
练习次数:0次
- 2011全国硕士研究生入学考试《数学2》真题
试卷分类:数学二
练习次数:0次
- 2010全国硕士研究生入学考试《数学2》真题
试卷分类:数学二
练习次数:0次
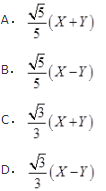

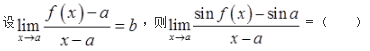
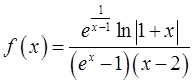 ,则(x)第二类间断点的个数为( )
,则(x)第二类间断点的个数为( )
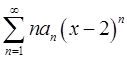 的收敛区间为(-2,6),则
的收敛区间为(-2,6),则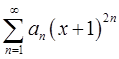 的收敛区间为( )。
的收敛区间为( )。


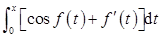 是奇函数。故应选A项。
是奇函数。故应选A项。