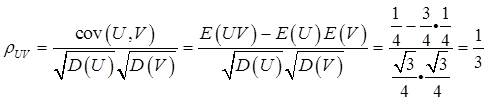设奇函数(x)在(-∞,+∞)上具有连续导数,则( )。

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:A
- 您的答案:
参考解析:
因为(x)在(-∞,+∞)上具有连续导数,且为奇函数,故′(x)为偶函数,又cos(x)也为偶函数,从而cos(t)+′(t)为偶函数,进而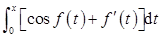 是奇函数。故应选A项。
是奇函数。故应选A项。
设幂级数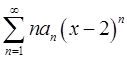 的收敛区间为(-2,6),则
的收敛区间为(-2,6),则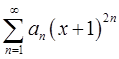 的收敛区间为( )。
的收敛区间为( )。
- A (-2,6)
- B (-3,1)
- C (-5,3)
- D (-17,15)
- 参考答案:B
- 您的答案:
参考解析:


设4阶矩阵A=(aij)不可逆,元素a12对应的代数余子式A12≠0,a1,a2,a3,a4为矩阵A的列向量组,A*为A的伴随矩阵,则A*x=0的通解为( )
- A x=k1a1+k2a2+k3a3,其中k1,k2,k3为任意常数
- B x=k1a1+k2a2+k3a4,其中k1,k2,k3为任意常数
- C x=k1a1+k2a3+k3a4,其中k1,k2,k3为任意常数
- D x=k1a2+k2a3+k3a4,其中k1,k2,k3为任意常数
- 参考答案:C
- 您的答案:
参考解析:
由A不可逆知,r(A)<4,又元素a12对应的代数余子式A12≠0,故r(A)≥3,从而r(A)=3。
由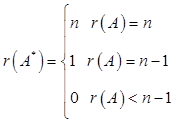 ,可知r(A*)=1。
,可知r(A*)=1。
故A*x=0的基础解系含有3个解向量。
因a1,a2,a3,a4为矩阵A的列向量组,则a1,a3,a4可看做作A12对应矩阵列向量组的延长组,故a1,a3,a4线性无关。
又A*A=A*(a1,a2,a3,a4)=|A|E=0,故a1,a3,a4均为A*x=0的解。
综上,a1,a3,a4为A*x=0的一个基础解系,故A*x=0得通解为x=k1a1+k2a3+k3a4,其中k1,k2,k3为任意常数。
设A为3阶矩阵,a1,a2为A的属于特征值1的线性无关的特征向量,a3为A的属于特征值-1的特征向量,则满足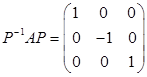 得可逆矩阵P为( )
得可逆矩阵P为( )
- A (a1+a3,a2,-a3)
- B (a1+a2,a2,-a3)
- C (a1+a3,-a3,a2)
- D (a1+a2,-a3,a2)
- 参考答案:D
- 您的答案:
参考解析:
a1,a2是A属于特征值1的线性无关的特征向量,即Aa1=a1,Aa2=a2,故A(a1+a2)=a1+a2,即a1+a2也是A属于特征值1的特征向量。
设k1(a1+a2)+k2a2=0,即k1a1+(k1+k2)a2=0,
由于a1,a2线性无关,故k1=k2=0,即a1+a2,a2线性无关。
a3是A属于特征值-1的特征向量,即Aa3=-a3,因此A(-a3)=-(-a3),即-a3也是A属于特征值-1的特征向量
可取P=(a1+a2,-a3,a2),则P是可逆矩阵,且满足。
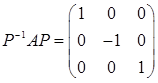
故应选D项。
若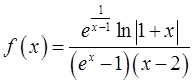 ,则(x)第二类间断点的个数为( )
,则(x)第二类间断点的个数为( )
- A 1
- B 2
- C 3
- D 4
- 参考答案:C
- 您的答案:
参考解析:

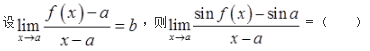
- A bsina
- B bcosa
- C bsin(a)
- D bcos(a)
- 参考答案:B
- 您的答案:
参考解析:
由拉格朗日中值定理知,存在ξ介于a与(x)之间,使得sin(x)-sina=cosξ·[(x)-a]。
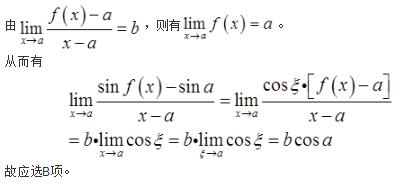
设A,B,C为三个随机事件,且P(A)=P(B)=P(C)=1/4,P(AB)=0,P(AC)=P(BC)=1/12,则A,B,C恰有一个事件发生的概率为( )
- A 3/4
- B 2/3
- C 1/2
- D 5/12
- 参考答案:D
- 您的答案:
参考解析:

设随机变量(X,Y)服从二维正态分布N(0,0;1,4;-1/2),下列随机变量中服从标准正态分布且与X独立的是( )
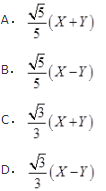
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:

设z=arctan[xy+sin(x+y)],则dz|(0,π)=
- 参考答案:(π-1)dx-dy
- 您的答案:
参考解析:

- 参考答案:y=x-1
- 您的答案:
参考解析:
Q表示产量,成本C(Q)=100+13Q,单价为p,需求量Q(p)=800/(p+3)-2。则工厂取得利润最大值时得产量
- 参考答案:Q=8
- 您的答案:
参考解析:
设平面区域D={(x,y)|x/2≤y≤1/(1+x^2),0≤x≤1},则D绕y周旋转所成旋转体体积为
- 参考答案:πln2-π/3
- 您的答案:
参考解析:
设随机变量X的概率分布为P{X=k}=1/2^k(k=1,2…),Y表示X除以3的余数,则EY=
- 参考答案:8/7
- 您的答案:
参考解析:
行列式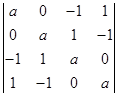 =
=
- 参考答案:
- 您的答案:
参考解析:
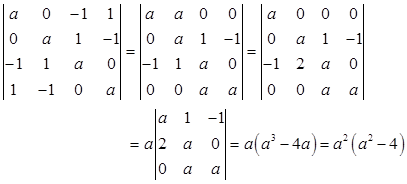

- 参考答案:
- 您的答案:
参考解析:


设A为2阶矩阵,P=(a,Aa),其中a是非零向量,且不是A的特征向量。
(Ⅰ)证明P为可逆矩阵;
(Ⅱ)若A2a+Aa-6a=0,求P^-1AP并判断A是否相似于对角阵。
- 参考答案:
- 您的答案:
参考解析:

设某种元件的使用寿命T的分布函数为: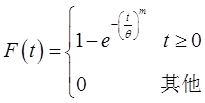 ,其中θ,m为参数且大于零。
,其中θ,m为参数且大于零。
(Ⅰ)求概率P{T>t}与P{T>s+t|T>s},其中s>0,t>0;
(Ⅱ)任取n个这个元件做寿命试验,测得它们的寿命分别为t1,t2,…tn,若m已知,求θ的最大似然估计值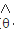 。
。
- 参考答案:
- 您的答案:
参考解析:
(Ⅰ)
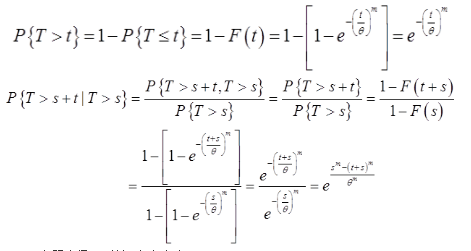
(Ⅱ)由题意得,T的概率密度为
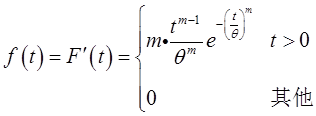
似然函数
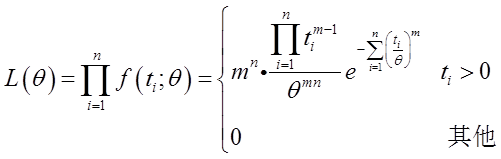
当ti>0时,
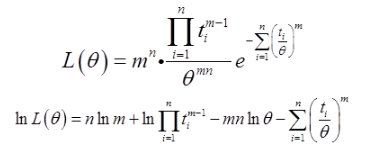
令
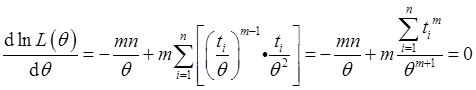
解之得θ的最大似然估计值为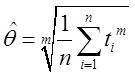 。
。
已知(1+1/n)^n-e与b/n^a为n→∞时的等价无穷小,求a,b。
- 参考答案:
- 您的答案:
参考解析:
由题意有
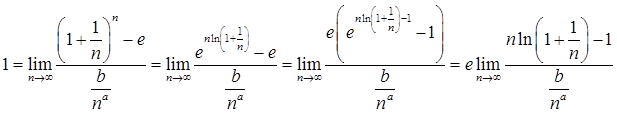
令1/n=t,则
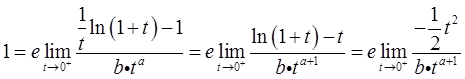
从而a+1=2,-e/(2b)=1,解之得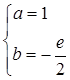 。
。
求(x,y)=x^3+8y^3-xy的极值。
- 参考答案:
- 您的答案:
参考解析:

已知y=(x)满足y″+2y′+5(x)=0,且有(0)=1,′(0)=-1。
(Ⅰ)求(x);
(Ⅱ)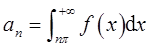 ,求
,求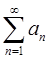 。
。
- 参考答案:
- 您的答案:
参考解析:

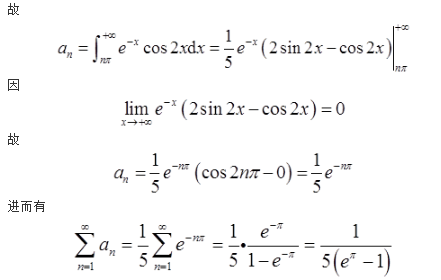
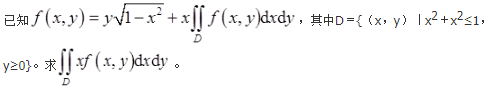
- 参考答案:
- 您的答案:
参考解析:
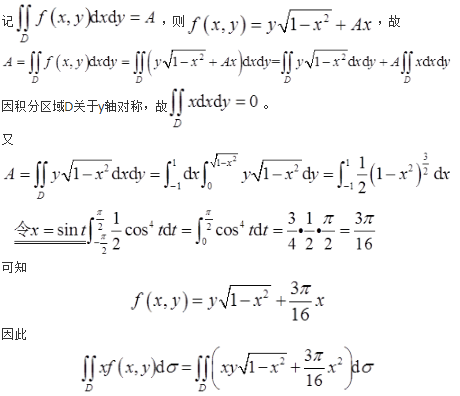

设(x)在区间[0,2]上具有一阶连续导数,且(0)=(2)=0,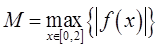 。
。
证明:(Ⅰ)存在ξ∈(0,2,)使得|′(ξ)|≥M;
(Ⅱ)若对任意x∈(0,2),|′(x)|≤M,则M=0。
- 参考答案:
- 您的答案:
参考解析:


已知因(X,Y)服从区域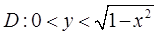 上的均匀分布,且
上的均匀分布,且
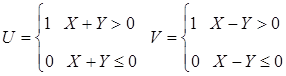
求:(Ⅰ)(U,V)的联合分布;
(Ⅱ)ρUV。
- 参考答案:
- 您的答案:
参考解析:
(Ⅰ)因(X,Y)服从区域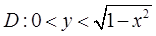 上的均匀分布,故
上的均匀分布,故
P{U=0,V=0}=P{X+Y≤0,X-Y≤0}=1/4,
P{U=0,V=1}=P{X+Y≤0,X-Y>0}=0,
P{U=1,V=0}=P{X+Y>0,X-Y≤0}=1/2,
P{U=1,V=1}=P{X+Y>0,X-Y>0}=1/4。
从而(U,V)的概率分布为
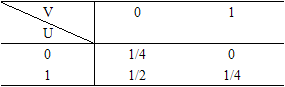
(Ⅱ)由(Ⅰ)知,
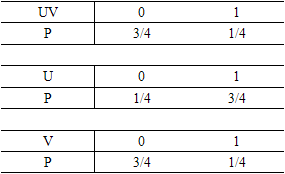
故E(UV)=1/4,E(U)=3/4,E(V)=1/4,D(U)=3/16,D(V)=3/16。
从而