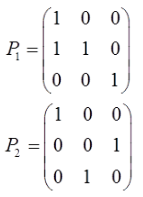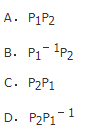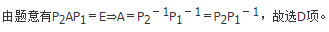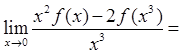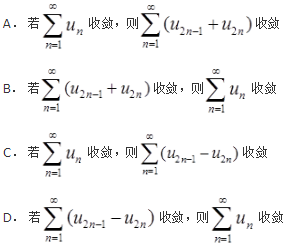2011年全国硕士研究生入学考试《数学三》真题

试卷预览

单选题

设总体X服从参数为λ（λ＞0）的泊松分布，X1，X2，…，Xn（n≥2）为来自该总体的简单随机样本，则对于统计量

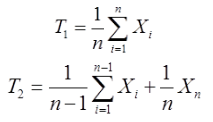
有（　　）。

查看答案开始考试

正确答案：D

本题解析：

由X1，X2，…，Xn～P（λ）知EXi＝λ，DXi＝λ，i＝1，2，…，n。从而

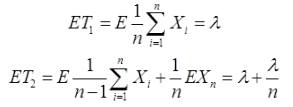
所以ET1＜ET2。

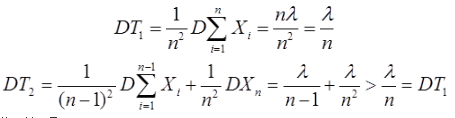
从而选D项。

单选题

设F1（x），F2（x）为两个分布函数，其相应的概率密度f1（x），f2（x）是连续函数，则必为概率密度的是（　　）。

查看答案开始考试

正确答案：D

本题解析：

易知，四个选项均满足大于等于零的条件。对选项D

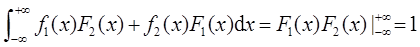
从而D项满足连续分布概率密度的条件，为概率密度，而其他选项均无法验证满足（－∞，＋∞）上积分为1的条件，故选D。

单选题

设A为4×3矩阵，η1，η2，η3是非齐次性方程组Ax＝β的三个线性无关的解，k1，k2为任意实数，则Ax＝β的通解为（　　）。

查看答案开始考试

正确答案：C

本题解析：

Ax＝β的一个解为（η2＋η3）/2，而η1，η2，η3线性无关，从而η3－η1，η2－η1也线性无关，且都为Ax＝0的解，从而原方程的通解可表示为（η2＋η3）/2＋k1（η2－η1）＋k2（η3－η1），故选C项。

单选题

设A为三阶矩阵，将A的第二列加到第一列得矩阵B，再交换B的第二行与第三行得到单位矩阵，记

则A＝（　　）。

查看答案开始考试

正确答案：D

本题解析：

单选题

设函数f（x）在x＝0处可导，且f（0）＝0，则

查看答案开始考试

正确答案：B

本题解析：

单选题

已知当x→0时，函数f（x）＝3sinx－sin3x与cxk是等价无穷小，则（　　）。

查看答案开始考试

正确答案：C

本题解析：

因为

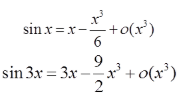
所以f（x）＝4x3＋ο（x3）～4x3，于是c＝4，k＝3，故选C项。

单选题

设

则I，J，K的大小关系为（　　）。

查看答案开始考试

正确答案：B

本题解析：

x∈（0，π/4），有sinx＜cosx＜1＜cotx，则lnsinx＜lncosx＜0＜lncotx，故

即I＜K＜J，故选B项。

单选题

设{un}是数列，则下列命题正确的是（　　）。

查看答案开始考试

正确答案：A

本题解析：

其他考生还关注了更多 +

• 全国硕士研究生入学考试《数学2》模拟试卷7

  试卷分类：数学二

  练习次数：0次

• 全国硕士研究生入学考试《数学2》模拟试卷6

  试卷分类：数学二

  练习次数：0次

• 全国硕士研究生入学考试《数学2》模拟试卷5

  试卷分类：数学二

  练习次数：0次

• 全国硕士研究生入学考试《数学2》模拟试卷4

  试卷分类：数学二

  练习次数：0次

• 全国硕士研究生入学考试《数学2》模拟试卷3

  试卷分类：数学二

  练习次数：0次

• 全国硕士研究生入学考试《数学2》模拟试卷2

  试卷分类：数学二

  练习次数：0次

• 全国硕士研究生入学考试《数学2》模拟试卷1

  试卷分类：数学二

  练习次数：0次

• 2012全国硕士研究生入学考试《数学2》真题

  试卷分类：数学二

  练习次数：0次

• 2011全国硕士研究生入学考试《数学2》真题

  试卷分类：数学二

  练习次数：0次

• 2010全国硕士研究生入学考试《数学2》真题

  试卷分类：数学二

  练习次数：0次