“三角形的中位线”是初中学习三角形知识点中必不可少的内容。对-名校题库网

题目详情

全站导航

首页试卷库试题库

试卷导航

学历类职业资格公务员医卫类建筑工程外语类计算机类财会类

试题导航

学历类职业资格公务员医卫类建筑工程外语类计算机类财会类

“三角形的中位线”是初中学习三角形知识点中必不可少的内容。对学生的要求是必须了解三角形中位线的概念，熟练掌握三角形中位线定理的证明和有关应用。

(1)该课程设定需要使学生达到什么能力目标

(2)本课程的教学重点与难点。

(3)教学过程(只要求写出新课导入和新知识探究、巩固、应用等)及设计意图。

正确答案及解析

正确答案

解析

(1)该课程设定需要使学生达到：

①经历“探索一发现一猜想一证明”的过程，进一步发展推理论证能力。

②能够用多种方法证明三角形的中位线定理，体会在证明过程中所运用的归纳、类比、转化等数学思想方法。

③能够应用三角形的中位线定理进行有关的论证和计算，逐步提高学生分析问题和解决问题的能力。

(2)教学重点与难点

教学重点：三角形中位线的概念与三角形中位线定理的证明。

教学难点：三角形中位线定理的多种证明。

(3)教学过程

①一道趣题——课堂因你而和谐

问题：你能将任意一个三角形分成四个全等的三角形吗这四个全等三角形能拼凑成一个平行四边形吗 (板书)

(这一问题激发了学生的学习兴趣，学生积极主动地加入到课堂教学中，课堂气氛变得较为和谐，课堂也鲜活起来了。)

学生想出了这样的方法：顺次连接三角形每两边的中点，看上去就得到了四个全等的三角形。将AADE绕E点沿顺(逆)时针方向旋转l800可得平行四边形ADFE。

问题：你有办法验证吗

②一种实验——课堂因你而生动

学生的验证方法较多．其中较为典型的方法如下：生l：沿DE、DF、EF将画在纸上的AABC剪开，看四个三角形能否重合。生2：分别测量四个三角形的三边长度，判断是否可利用“SSS”来判定三角形全等。生3：分别测量四个三角形对应的边及角，判断是否可用“SAS、ASA或AAS”判定全等。

引导：上述同学都采用了实验法，存在误差，那么如何利用推理论证的方法验证呢

③一种探索——课堂因你而鲜活

师：把连接三角形两边中点的线段叫做三角形的中位线。(板书)

问题：三角形的中位线与第三边有怎样的关系呢在前面图l中你能发现什么结论呢 (学生的思维开始活跃起来，同学之间开始互相讨论，积极发言)

中学数学学科知识与教学能力,预测试卷,2021年教师资格证考试《数学学科知识与教学能力》（初级中学）预测试卷3

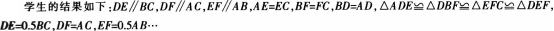
猜想：三角形的中位线平行于第三边，且等于第三边的一半。(板书)

师：如何证明这个猜想的命题呢

生：先将文字问题转化为几何问题然后证明。

已知：DE是ABC的中位线，求证：DE／／BC、DE--0．5BC。学生思考后教师启发：要证明两条直线平行，可以利用。三线八角”的有关内容进行转化，而要证明一条线段的长等于另一条线段长度的一半，可采用将较短的线段延长一倍，或者截取较长线段的一半等方法进行转化归纳。(学生积极讨论，得出几种常用方法．大致思路如下)

生l：延长DE到F使EF=DE．连接CF

中学数学学科知识与教学能力,预测试卷,2021年教师资格证考试《数学学科知识与教学能力》（初级中学）预测试卷3

问题：三角形的中位线与中线有什么区别与联系呢

容易得出如下事实：都是三角形内部与边的中点有关的线段。但中位线平行于第三边，且等于第三边的一半，三角形的一条中位线与第三边上的中线互相平分。(学生交流、探索、思考、验证)

⑤一种照应——课堂因你而完整

问题：你能利用三角形中位线定理说明本节课开始提出的趣题的合理性吗 (学生争先恐后回答．课堂气氛活跃)

⑥一句总结——课堂因你而彰显无穷魅力

学生总结本节内容：三角形的中位线和三角形中位线定理。(另附作业)

⑦课后反思

本节课以“如何将一个任意三角形分为四个全等的三角形”这一问题为出发点，以平行四边形的性质定理和判定定理为桥梁，探究了三角形中位线的基本性质和应用。在本节课中，学生亲身经历了“探索一发现一猜想一证明”的探究过程，体会了证明的必要性和证明方法的多样性。在此过程中，笔者注重新旧知识的联系，同时强调转化、类比、归纳等数学思想方法的恰当应用，达到了预期的目的。