设A是一个mxn矩阵，证明：矩阵A的行空间维数等于它的列空间维数。
正确答案及解析
正确答案
解析
证明
设矩阵行空间的维数为r，列空间维数为rl’ α1，α2，…αn为矩阵A的行向量组，不妨设αl，α2，…αγ为一组基所以方程组
只有零解．
即线性方程绸
只有零解，
则其系数矩阵
的行向量空间的维数≥r， 因此它的行向量组可以找到r个线性无关的向量，不妨设为
也线性无关．它们正好是矩阵A的r个列向量，则矩阵A的列空间的维数r。≥r。
同理可证r≥rl，所以r=n，即矩阵A行空间的维数等于它列空间的维数。
包含此试题的试卷
你可能感兴趣的试题
案例：阅读下列教学片段。
呈现问题情境：某股民在上星期五以每股27元的价格买进某股票1000股。该股票的涨跌情况如下表(单位：元)。
师：星期四收盘时，每股多少元
提问生1、2(疑惑不解状)。
生3：27—2．5=25．5(元)。
师：星期四收盘价实际上就是求有理数的和，应该为：27+4+4．5—1—2．5=32(元)。
师：周二收盘价最高为35．5元；周五最低为26元。
师：已知该股民买进股票时付了3％0的交易税，卖出股票时需付成效额3％0的手续费和2‰的交易税。如果该股民在星期五收盘前将全部股票卖出，他的收益情况如何
提问生4、5(困惑状)。
生6：买入：27×1000x(1+3％0)=27081(元)；
卖出：26×1000×(1+3‰+2‰)=26130(元)；
收益：26130—27081=一951(元)。
师：生6的解答错了，正确解答为：：
买入股票所花费的资金总额为：27×1000x(1+3％o)=27081(元)；
卖出股票时所得资金总额为：26×1000×(1—3％0～2％o)=25870(元)；
上周交易的收益为：25870—27081=一1211(元)，实际亏损了l 211元。
师：请听明白的同学举手。
此时课堂上约有三、四个学生举起了手，绝大部分学生眼中闪烁着疑惑之意。有些学生在窃窃私语，有一学生轻声道：“老师，我听不懂!”……少部分学生烦燥之意露于言表。
问题：
(1)案例中老师犯了什么错误
(2)该案例中学生的数学困惑是什么
(3)该案例的启示是什么
启示是什么
- 查看答案
初中“变量与函数”设定的教学目标如下：
①运用丰富的实例，使学生在具体情境中领悟函数概念的意义，了解常量与变量的含义．
能分清实例中的常量与变量，了解自变量与函数的意义：
②通过动手实践与探索，学生参与变量的发现和函数概念的形成过程．以提高分析问题和解决问题的能力：
③引导学生探索实际问题中的数量关系，培养对学习的兴趣和积极参与数学活动的热情。
在解决问题的过程中体会数学的应用价值并感受成功的喜悦。建立自信心。
完成下列任务：
(1)根据教学目标①，给出至少两个实例，并说明设计意图。
(2)根据教学目标②，给出至少两个实例，并说明设计意图。
(3)根据教学目标③，设计两个问题，并说明设计意图。
(4)本节课的教学重点是什么
(5)作为初中阶段的基础内容，其难点是什么
(6)本节课的教学内容对后续哪些内容的学习有直接影响
- 查看答案
目前我们的新课程改革已基本进行了一轮，从你的教学实践过程中，你觉得义务教育的数学课程标准中有哪些理念和内容，或者在我们具体执行课程标准的教学过程中有哪些做法，可以进行修改或改进 提出你的修改建议和理由。
- 查看答案
椭圆
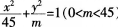的焦点分别是F1和F2，已知椭圆的离心率
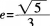．过中心O 作直线与椭圆交于A，B两点，O为原点，若△ABF2的面积是20。
(1)求m的值；
(2)直线AB的方程。
- 查看答案
设函数f(x)在定义域，上的导数大于零，若对任意的
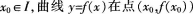
处的切线与直线x≈x0及戈轴所围成区域的面积恒为4，且f(0)=2，求f(x)的表达式。
- 查看答案