《义务教育数学课程标准(2011年版)》提出了“四基”的课程目标,“四基”的内容是什么 分别举例说明“四基”的含义。
正确答案及解析
正确答案
解析
“四基”的内容是:数学的基础知识、基本技能、基本思想、基本活动经验。
基础知识一般是指数学课程中所涉及的基本概念、基本性质、基本法则、基本公式等。比如,说明1,0.25和25%的含义。分数、小数和百分数是重要的数概念,它们有本身的特征,又有密切的联系。真分数通常表示部分与整体的关系,所以理解什么是1/4:一定要知道是哪个整体的,如全班同学人数的—l-。全班同学是40人,其是10人,全班同学是32人,其。l就是8人。小数通常表示具体的数量,如一支铅笔0.25元,书桌的宽度是0.45米。百分数是同分母(统一标准)的比值,便于比较,如去年比前年增长21%,今年比去年增长25%。
基本技能内容包括基本的运算、测量、绘图等技能。如20以内加减法和九九乘法表内乘法,每分钟完成8—10题。这一要求可以看作是一个参照,大多数学生经过一定的训练完全可以达到,不排除一些学生经过一段时间才能达到这一要求,也会有一些学生要高于这一要求。这一要求可以成为平时考查学生的参考,也可以作为测验和考试的参考。
数学基本思想主要是指数学抽象的思想、数学推理的思想和数学模型的思想。比如,数概念的形成与发展是数与代数中的重要内容,从整数、小数、分数到有理数的学习,是一个从具体事物和数量抽象为数的过程,是抽象水平不断提高的过程。教学中应当结合具体教学内容的学习,把抽象的思想体现在教学活动之中,培养学生的抽象思维能力。比如,最简单的l0以内数的认识,其中就蕴含了深刻的抽象的过程和抽象的思想。
数学基本活动经验的积累要和过程性目标建立联系。如《标准(2011年版)》规定,经历数与代数的抽象、运算与建模等过程。掌握数与代数的基础知识和基本技能;经历图形的抽象、分类、性质探讨、运动、位置确定等过程,掌握图形与几何的基础知识和基本技能;经历在实际问题中收集和处理数据、利用数据分析问题、获取信息的过程,掌握统计与概率的基础知识和基本技能。这些过程性目标和内容实现的主要标志就是学生形成活动经验.学生在经历相关的数学活动中.了解数学知识发生发展的过程,体会数学知识和方法的探究。
包含此试题的试卷
你可能感兴趣的试题
通过直观感知、操作确认,归纳出直线与平面垂直的判定定理:一个直线与一个平面内的两条相交直线垂直,则该直线与此平面垂直。
请你完成下列任务:
(1)请你设计一个探索该定理的活动或问题情境,并说明设计意图;(10 分)
(2)请你设计一个习题(不必解答),以帮助学生理解该定理,并说明具体的设计意图;(10 分)
(3)请你设计一个习题(不必解答),进一步巩固、应用该定理,并说明具体的设计意图。(10 分)
- 查看答案
下面是高中“集合”一章“集合的含义与表示”的部分教材内容:
在小学和初中,我们已经接触过一些集合,例如,自然数的集合,有理数的集合,不等式的解的集合,到一个定点的距离等于定长的点的集合(即圆),到一条线段的两个端点距离相等的点的集合(即这条线段的垂直平分线)…… 那么,集合的含义是什么呢?我们再来看下面的一些例子:
(1)1~20 以内的所有素数;
我国从 1991-2003 年的 13 年内所发射的所有人造卫星;
金星汽车厂 2003 年生产的所有汽车;
(4)2004 年 1 月 1 日之前与中华人民共和国建立外交关系的所有国家;
所有的正方形;
到直线 l 的距离等于定长 d 的所有的点;
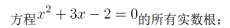
新华中学 2004 年 9 月入学的所有的高一学生。
例(1)中,我们把 1~20 以内的每一个素数作为元素,这些元素的全体就是一个集合;同样地,例(2) 中,把我国从 1991-2003 年的 13 年内发射的每一颗人造卫星作为元素,这些元素的全体也是一个集合。
【思考 1】
上面的例(3)到例(8)也都能组成集合吗?它们的元素分别是什么?
一般地,我们把研究对象统称为元素(element),把一些元素组成的总体叫作集合(set)(简称为集)。给定的集合,它的元素必须是确定的。也就是说,给定一个集合,那么任何一个元素在不在这个集合中就确定了。例如,
“中国的直辖市”构成一个集合,北家、上海、天津、重庆在这个集合中,杭州、南京、广州不在这个集合中。“身材较高的人”不能构成集合,因为组成它的元素是不确定的。
一个给定集合中的元素是互不相同的。也就是说,集合中的元素是不重复出现的。只要构成两个集合的元素是一样的,我们就称这两个集合是相等的。
【思考 2】
判断下列元素的全体是否組成集合,并说明理由:
大于 3 小于 11 的偶数;
我国的小河流。
我们通常用大写拉丁字母 A,B,C,…表示集合,用小写拉丁字母 a,b,c…表示集合中的元素。
如果 a 是集合 A 的元素,就说 a 属于(bedong to)集合 A,记作 a∈A;如果 a 不是集合 A 中的元素,就说 a 不属于(not belong to)集合 A,记作 aA。
例如,我们用 A 表示“1-20 以内的所有素数”组成的集合,则有 3∈A,4A,等等。问题:
阅读这段教材,概括与集合有关的新知识点;(6 分)
阅读这段教材中的【思考 2】,说明设置此栏目内容的主要意图;(6 分)
请说明集合在高中数学课程中的地位和作用。(8 分)
- 查看答案
给出基本不等式
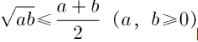
的一种几何解释,并说明几何解释对学生数学学习的作用
- 查看答案

