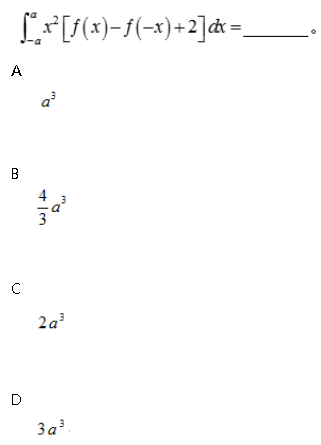
- A.A
- B.B
- C.C
- D.D
正确答案及解析
正确答案
解析

你可能感兴趣的试题
案例:
下面是一位老师在讲“指数函数及其性质探究”第一课“探究指数函数定义、图象及其性质”时的教学片段,请阅读后回答问题:
师:请同学们不断地沿同一方向对折一张长方形的纸。你能找出折叠的次数与某个变量之间的数量关系吗 为了简化问题,不妨假设纸的初始面积为单位1。
师:现在同学们开始做,请找出自变量是谁 自变量和那个变量之间的关系,关系式是什么 请大家以学习小组为单位进行探究。
生:我们探究的是折叠次数是自变量,折叠次数和纸的层数的关系式是y=2χ(这时教师在黑板上写上折叠次数χ:O 1 2 3……,下一行写上纸的层数y:1 2 4 8……)
师:还有没有同学找到了不同的关系式 请举手。
生:我们找的自变量也是折叠次数,折叠次数和纸的面积之间的关系式是y=(1/2)χ。(这时教师在黑板上写上折叠次数χ:0 1 2 3……,再下一行写上y:1 0.5 0.25 0.125……)
师:列出的这两个函数解析式的形式有什么共同特征 把它们的定义域扩充到全体实数后就成了一个新的函数,我们看自变量的位置在指数的位置,我们给这一类函数起名叫指数函数(这时候板书课题)。
问题:
(1)该教师在引入新课题时用了什么方法,对此你有何看法,并说明理由。(15分)
(2)请对该教师的课堂提问作出评析。(15分)
- 查看答案
高中“方程的根与函数的零点”(第一节课)设定的教学目标如下:
①通过对二次函数图象的描绘,了解函数零点的概念,渗透由具体到抽象思想,领会函数零点与相应方程实数根之间的关系;
②理解提出零点概念的作用,沟通函数与方程的关系。
③通过对现实问题的分析,体会用函数系统的角度去思考方程的思想,使学生理解动与静的辨证关系。掌握函数零点存在性的判断。完成下列任务:
(1)根据教学目标,设计一个问题引入,并说明设计意图;
(2)根据教学目标①,设计问题链(至少包含三个问题),并说明设计意图;
(3)根据教学目标③,给出至少一个实例和三个问题,并说明设计意图;
(4)确定本节课的教学重点;
(5)作为高中阶段的基础内容,其难点是什么
(6)本节课的教学内容对后续哪些内容的学习有直接影响
- 查看答案
给出中学几何研究图形的几个主要方法,并试以其中一种为例,说明该种方法的基本特点。
- 查看答案
一圆与y轴相切,圆心在x-3y=O上,在y=x上截得的弦长为2√7,求圆的方程。
- 查看答案
某煤矿发生透水事故时,作业区有若干人员被困。救援队从入口进入之后有L1,L2两条巷道通往作业区(如图),L1巷道有A1,A2,A3三个易堵塞点,各点被堵塞的概率都是争;L2巷道有日B1,B2两个易堵塞点,被堵塞的概率分别为3/4,3/5。
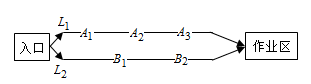
(1)求L1巷道中,三个易堵塞点最多有一个被堵塞的概率;
(2)若L2巷道中堵塞点个数为Χ,求Χ的分布列及数学期望EΧ,并按照“平均堵塞点少的巷道是较好的抢险路线“的标准,请你帮助救援队选择一条抢险路线,并说明理由。
- 查看答案