在一次数学课上.教师给出如下例题

正当老师要转入下一个例题的时候.有学生提出:能否从等式右边推导出等式左边?教师以从等式右边推导出左边 比较繁琐为理由,不理会学生,就匆匆进入了下一个例题的讲解。
问题:
(1)结合上述案例,谈一谈教师应如何看待学生提问不在教学预设的情况。(10 分)
(2)如果你是该教师,那么如何回答学生的提问?(10 分)
正确答案及解析
正确答案
解析
(1)教师应该区别对待学生提出的问题。首先,要判断学生问题的价值,依据价值性大小给与回应。我们把与教学 目标相关的问题都归为“正问题”。把偏离或背离教学目标的问题归为“负问题”。如本案例中学生的提问“能否 从等式右边推导出等式左边”这一问题便是“正问题”,对待“正问题”应该给与积极回应。对学生提出的“负问 题”,教师一方面可以启发引导,将其转化成“正问题”进行处理,一方面可以采取“冷处理”的办法。其次,要 依据问题的内容灵活进行,如师生互动讨论或生生小组讨论,也可以让学生自行探究或课下解决。 (2)如果我是该教师我会将该问题作为一道思考题目,让学生进行小范围的讨论,最后对此三种解题方式进行分析 总结。具体实施方式如下: 问题 1:刚刚这位同学提出了一个很新颖的解题思路。那么我们可不可以从等式右边推导出等式左边呢?大家同桌之 间讨论一下,可不可以,又是如何推导的呢? 我将在学生讨论的过程中,进行巡视并对有问题的学生加以指导,为了不耽误课堂进度,讨论时间初步预设为 3 分 钟。提问.请学生进行结果展示
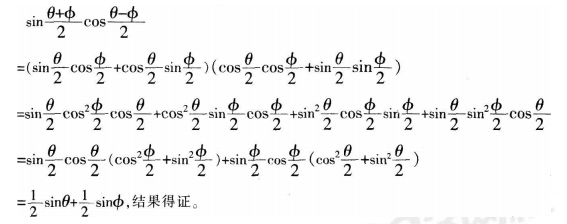
提问:对比三种解决方法,各自的优点是什么?谈一谈你更倾向于用哪种方法解决问题? 引导学生共同总结:在解决三角函数公式证明题的时候,①合理的选择诱导公式以及和差化积公式非常的重要,如: 方法三对于两角和差公式的反复运用,虽计算过程稍微复杂,但是方法更加的简单,容易想到。②能够灵活的运用 整体代换的思想方法快速解决问题,如:方法一、方法二可以精简计算过程,避免计算出错。