设三维空间中椭圆
(1)证明T的中心为原点，并求，的长轴和短轴的长度。(5分)
(2)证明：任给一个椭圆，存在参数R和k，使得T与给定椭圆全等。(5分)
正确答案及解析
正确答案
解析
(1)由已知得，椭圆，为圆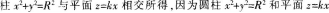
的中心都为原点．故椭圆，的巾心为原点。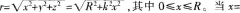 
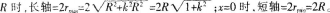
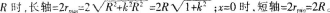(2)以椭圆f长轴所在直线为横轴m，短轴所在直线为纵轴n建立直角坐标系，可得f的方程为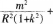
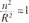．其中长短轴之比为
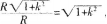与R无关。故对任意给定的一个椭圆(其长半轴和短半轴分别为a．b)．均可找到参数k，R使得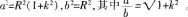
包含此试题的试卷
你可能感兴趣的试题
平方差公式
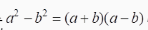
是初中乘法公式的内容之一。
某教师教学时，将引导学生归纳猜想平方差公式作为教学过程的环节之一，设计思路如下:
假定b=1。问题简化为：a2-1=?
(1)问答题简述该教师在该环节的问答题意图。
(2)问答题简述平方差公式在初中数学中的地位。
(3)问答题请给出平方差公式的教学目标，并设计教学流程
(4)问答题请通过图示给出平方差公式的几何背景
- 查看答案
案例:
下面是初中"三角形的内角和定理”的教学案例片段。教师请学生回忆小学学过的三角形内角和是多少度？并让学生用提前准备好的三角形纸片进行剪拼并演示。下面是部分学生演示的图形 (如图1、图2) :
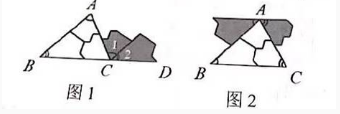
在图1中，三角形的三个内角拼在一起后， B、C、D在一条直线上，看似构成一个平角。教师质疑，看上去是平角就是平角了吗？学生的回答是”不一定”。接着，教师利用图1启发学生思考:
①既然不能判定B、C、D是否一定在同一直线上(即组成平角)，可以换个角度，先构造一个平角，引导学生结合图1思考如何作辅助线构造平角。 学生想到了作BC的延长线BD，如图3所示。
②图1中，∠1与∠A是什么关系?启发学生在∠ACD内作∠1=∠A，或过点C作CE//AB，如图4所示。
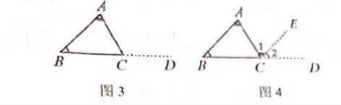
③现在只要证明什么？(证明∠2=∠B）
问题：
（1）该教师让学生回忆并用拼图的方法感知三角形的内角和，请简述其教学意图。
（2）利用图2设计问题串，使得这些问题能够引导学生发现三角形的内角和定理的证法。
（3）请再给出其他2种三角形纸片的拼法，并画图表示
- 查看答案
数学运算能力是中学数学教学需要培养的基本能力。学生的数学运算能力具体表现为哪些方面?请以整式运算为例予以说明。
- 查看答案
已知非齐次线性方程组
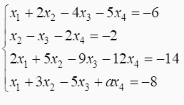
（1）a为何值时，其对应齐次线性方程组解空间的维数为2?
（2）对于(1)中确定的a值，求该非齐次线性方程组的通解。
- 查看答案
已知方程组：
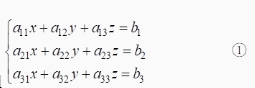
有惟一解当且仅当行列式
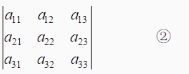
不等于零
请回答下列问题:
（1）行列式②的几何意义是什么?
（2）上述结论的集合意义是什么？
- 查看答案