以下是某教师对《矩形》一课进行的教学设计：
(一)观察思考，形成概念
1．形成概念：
学生具备了一定的逻辑思维推理能力，但还是以形象思维为主，因此我运用课件展示平行四边形形状变化动态，在小组内运用活动的平行四边形教具观察变化，提出猜想，概括定义。为了让学生向概念形成集中思维，我给出三个引导性问题。
(1)每次变化后还是平行四边形吗?
(2)变化过程中，哪些量不变?哪些量变?怎样变?
(3)变化过程中有没有一个形状特殊的平行四边形?怎样特殊?
这样，学生经历了概念的形成，进一步培养了观察能力和概括能力。
2．理解概念：
判断：(1)平行四边形是矩形。
(2)有一个角是900的四边形是矩形。
(3)矩形是平行四边形。
(二)观察猜想，探索性质
在这一环节。我通过两个探究活动，采用直观演示、小组合作探究、分组讨论的教学方法，引导学生去探究矩形的性质及推论。
探究：拿出一张矩形纸片。
?
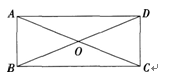
1．除了具有平行四边形的所有性质外，它的边、角、对角线还有哪些特殊性质呢?
2．有对称性吗?
3．你能用什么方法说明你的结论是正确的?性质l：矩形的四个角都是直角。
性质2：矩形的对角线相等。
让学生先独立思考，操作2、3分钟后，前后四人为一个小组，共同观察、讨论、猜想、验证。我将参与小组的讨论，积极地看、积极地听，感受学生的所思所想，根据情况随时进行指导，特另q是对学习有困难的同学倍加关切。
当学生探究矩形对角线相等的性质遇到困难时，我让学生观察在平行四边形演变为矩形的过程中，对角线的变化情况，进而猜测两条对角线的数量关系，如个别小组仍有f,'-1题，我会引导他们画对角线．利用测量、折叠等方法来探究。
为了诱导推论，我让学生观察矩形ABCD，用多媒体课件演示从矩形中抽象出直角三角形，引导学生归纳推论。因为文字叙述很难，我做进一步的引导：AC是Rt△ABC的什么边?OB是AC边上的什么线?，那么此结论应该怎样叙述?学生探索回答后，师生共同归纳，论证推论。(1)推论：直角三角形斜边上的中线等于斜边的一半。
(2)总结直角三角形的性质。
针对上述材料，完成下列任务。
(1)请分析该教师对矩形的性质推论教学设计片段的设计意图。(6分)
(2)请认真学习此教师的教学设计并为协助其完成一个本节课的课堂小结，并说明设计思路。(8分)
(3)除上述几个环节以外，你认为还可以添加哪些环节辅助教学呢?举例说明并作出简要设计。(16分)
正确答案及解析
正确答案
解析
(1)让学生感受矩形与直角三角形有密切的关系，引导学生归纳总结直角三角形的性质，有助于学生形成系统化的知识，培养良好的学习习惯。 (2)归纳小结，反思收获①知识结构图：
②矩形不同于平行四边形的2条性质及推论。
③解题指导：矩形问题一直角三角形或等腰三角形
④注意知识之间相互联系、相互转化、相互渗透以及辩证关系的挖掘，以运动的观点来认识事物之间的内在联系。
课堂小结是从结构、知识、方法、数学思想等四个方面设计。使学生理清所学知识的脉络和使用方法，对所学知识和方法有一个全面、系统的认识，便于从所学众多知识中，归纳出解决同一问题的一般规律。
(3)①课堂检测
用四道比较基础的填空题了解学生对本堂课知识与方法的掌握情况。
a．矩形的两条对角线的夹角为600，一条对角线与短边的和为l5，对角线长是． ，两边长分别等于 。
b．在直角三角形ABC中，∠C=900，AB=2AC，则∠A ＝__________，∠B=__________。
c．已知矩形ABCD中，D是AC，BD的交点，0C=BC，则∠CAB＝__________
d．已知矩形对角线长为8 cm，一边长为4 cm，则矩形的面积是 。
②作业设计
目的是巩固所学知识，发现和弥补学生在学习中的遗漏和困惑，强化基本技能训练，设计了必做题和选做题，使不同层次学生均有所收获，体现因材施教。
必做题：a．人教版教材P53练习l、2、3。
b．思考：平行四边形有一个角是直角会成为矩形，那么有一组邻边相等将会是什么图形 你能对比探究性质吗
选做题：四边形ABCD中，LABC=LADC=900，E为AC的中点，EF平分LBED交BD于F，请你猜证EF与BD的关系。
包含此试题的试卷
你可能感兴趣的试题
案例：阅读下列有关“_元一次方程的实践与探索”教学片段。
(多媒体展示)学校需要制作一块广告牌，请来两名工人。已知师傅单独完成需4天，徒弟
单独完成需6天，两人合作需要几天完成
解：设两人合作需要x天完成，根据题意列方程：
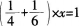
解方程．得x=2．4。
答：师徒两人合作需要2．4天完成任务。
师：同学们对本题还有疑问么
生：没有了!
(情境拓展)
师：真没有了 同学们想不想试着提出其他的问题来考考大家呢 如果想，请把问题写下来。
教师的话引起了学生们的兴趣，学生个个跃跃欲试。
稍后。教师在整理学生们的问题的过程中，发现有的学生按照教科书的提示出了这样一个
问题。
(1)学校需要制作一块广告牌，请来两名工人。已知师傅单独完成需4天，徒弟单独完成需6天．一人先做一天再和另一人合作，需几天完成
生1：这个问题简单，把一人先做的量从总量中扣掉不就行了。
师：你的想法很好!
生2(迫切地举手)：老师，这道题出错了!问题说“一人先做”，可是没说哪个人先做啊。
生3：对，可能是师傅先做，也可能是徒弟。所以我们得分两种情况来解决这个问题!
生3的回答赢得了师生们热烈的掌声，解答过程略。)
师：老师想把这个问题略加改动，还有信心挑战吗
生(齐声)：有!
(多媒体展示)
(2)学校需要制作一块广告牌，请来两名工人。已知师傅单独完成需4天，徒弟单独完成需6天．两人先合作一天再一人单做，几天完成
很快．不少同学积极举手，脸上露出自信的表情。
生4：我发现问题(1)是先独做再合作，而问题(2)则正好相反。所以只要将两人合作的工作量扣掉就可以了。
生5：跟问题(1)类似，我们也要分两种情况解决。
师(a-出欣慰的笑容)：／两4-#-．-"同学的分析太精彩了!看来大家已经感受到了数学中的分类讨论思想。现在老师看看同学4r1-还提出了什么问题。
此时学生情绪高涨，期待老师展示下一个题目。
(多媒体展示)
(3)学校需要制作一块广告牌，请来两名工人。已知师傅单独完成需4天，徒弟单独完成需6天，两人合作，完成后共得报酬l 000元，如果按个人完成的工作量计算报酬，那么该如何分配
生6(按捺不住兴奋)．这个问题太简单了，师傅和徒弟的工作效率之比是6：4，所以师傅应得600元，徒弟应得400元。
师：你能灵活地应用师徒二人的工作效率之间的关系来解答此题，思维很敏捷呀!
师(故作困惑)：现由徒弟先做l天，再由两人合作，完成后共得报酬450元。如果按个人完成的工作量计算报酬，那么又该如何分配
学生们认真思考着……
在问题(3)的启发下，许多学生对本题予以了正确解答。
问题：
(1)分析案例中教学过程的特点：
(2)根据案例内容，结合你的教学经历，说明创造性地使用数学教科书的原则。
- 查看答案
针对初中数学“二元一次方程”的内容，完成下列任务。
(1)写出“二元一次方程”这节课的教学目标以及重难点。
(2)设计一个与二元一次方程有关的例题，并说明你的设计意图。
(3)举例写出几个适合本节课教学的教法和学法。
- 查看答案
已知向量a，b，满足
其中k>0。
(1)试用k表示a·b，并求出a·b的最大值及此时aL5 b的夹角0的值：
(2)当a·b取得最大值时，求实数A，使la+Abl的值最小，并对这一结论作出几何解释。
- 查看答案
若方程
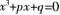的三个根是a、6、c，求证：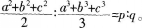
- 查看答案
设
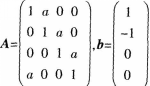(1)求lAl； (2)已知线性方程组AX-b有无穷多解，求a，并求AX=b的通解。
- 查看答案