在一条笔直公路一边有许多房子,现要安装消防栓,每个消防栓覆盖范围远大于房子面积,如下图所示。现求解能覆盖所有房子最少消防栓数和安装方案(问题求解过程中,可将房子和消防栓均视为直线上点)。该问题求解算法基本思路为:从左端第一栋房子开始,在其右侧m米处安装一个消防栓,去掉被该消防栓覆盖所有房子。在剩余房子中重复上述操作,直到所有房子被覆盖。算法采用设计策略为( );对应时间复杂度为( )。

假设公路起点A坐标为0,消防栓覆盖范围(半径)为20米,10栋房子坐标为(10,20,,30,35,60,80,160,210,260,300),单位为米。根据上述算法,共需要安装(请作答此空)个消防栓。以下关于该求解算法叙述中,正确是( )。
- A.4
- B.5
- C.6
- D.7
正确答案及解析
正确答案
解析
对于第一空,本题使用是分治法。1、分治法特征:对于一个规模为n问题,若该问题可以容易地解决(比如说规模n较小)则直接解决;否则将其分解为k个规模较小子问题,这些子问题互相独立且与原问题形式相同,递归地解这些子问题,然后将各子问题解合并得到原问题解。2、动态规划法:在求解问题中,对于每一步决策,列出各种可能局部解,再依据某种判定条件,舍弃那些肯定不能得到最优解局部解,在每一步都经过筛选,以每一步都是最优解来保证全局是最优解。本题情景没有列出所有可能解进行筛选,因此,本题不属于动态规划法。3、回溯法:回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当搜索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择。这种走不通就退回再走技术就是回溯法。本题情景没有探索和回退过程,因此,本题不属于回溯法。4、贪心法:总是做出在当前来说是最好选择,而并不从整体上加以考虑,它所做每步选择只是当前步骤局部最优选择,但从整体来说不一定是最优选择。由于它不必为了寻找最优解而穷尽所有可能解,因此其耗费时间少,一般可以快速得到满意解,但得不到最优解。在本题情景中,没有给出每步选择局部最优判断条件,因此,本题属于贪心法。 由于本题算法过程,是依次与各个房子进行判断,当所有房子都被比较之后,则问题结束,因此时间复杂度与房子个数相关,本问题时间复杂度应该趋于现象,为O(n)。对于第三空,关于对应序列(10,20,30,35,60,80,160,210,260,300)第一轮放置:在第一座房子x=10右侧20米处安装一个消防栓,可以覆盖10,20,30,35这4栋房子;2、第二轮放置:去掉前4栋房子,在第5栋房子x=60右侧20米处安装一个消防栓,可以覆盖60、80这2栋房子;3、第三轮放置:去掉前面已覆盖房子,在第7栋房子x=160右侧20米处安装一个消防栓,只可以覆盖160这一栋房子;4、第四轮放置:去掉前面已覆盖房子,在第8栋房子x=210右侧20米处安装一个消防栓,可以覆盖210这一栋房子第五轮放置:去掉前面已覆盖房子,在第9栋房子x=260右侧20米处安装一个消防栓,可以覆盖260、300这2栋房子;房子全部覆盖完毕,因此共需安装5个消防栓。对于第四空,对于得到一个最优解是动态规划特点,可以得到问题所有最优解,是回溯法特征,可以排除A、B选项。对于C、D选项。A.肯定可以求得问题一个最优解B.可以求得问题所有最优解C.对有些实例,可能得不到最优解D.只能得到近似最优
你可能感兴趣的试题
在一条笔直公路一边有许多房子,现要安装消防栓,每个消防栓覆盖范围远大于房子面积,如下图所示。现求解能覆盖所有房子最少消防栓数和安装方案(问题求解过程中,可将房子和消防栓均视为直线上点)。该问题求解算法基本思路为:从左端第一栋房子开始,在其右侧m米处安装一个消防栓,去掉被该消防栓覆盖所有房子。在剩余房子中重复上述操作,直到所有房子被覆盖。算法采用设计策略为( );对应时间复杂度为( )。

假设公路起点A坐标为0,消防栓覆盖范围(半径)为20米,10栋房子坐标为(10,20,,30,35,60,80,160,210,260,300),单位为米。根据上述算法,共需要安装( )个消防栓。以下关于该求解算法叙述中,正确是(请作答此空)。
-
- A.肯定可以求得问题一个最优解
- B.可以求得问题所有最优解
- C.对有些实例,可能得不到最优解
- D.只能得到近似最优解
- 查看答案
在一条笔直公路一边有许多房子,现要安装消防栓,每个消防栓覆盖范围远大于房子面积,如下图所示。现求解能覆盖所有房子最少消防栓数和安装方案(问题求解过程中,可将房子和消防栓均视为直线上点)。该问题求解算法基本思路为:从左端第一栋房子开始,在其右侧m米处安装一个消防栓,去掉被该消防栓覆盖所有房子。在剩余房子中重复上述操作,直到所有房子被覆盖。算法采用设计策略为( );对应时间复杂度为( )。

假设公路起点A坐标为0,消防栓覆盖范围(半径)为20米,10栋房子坐标为(10,20,,30,35,60,80,160,210,260,300),单位为米。根据上述算法,共需要安装(请作答此空)个消防栓。以下关于该求解算法叙述中,正确是( )。
-
- A.4
- B.5
- C.6
- D.7
- 查看答案
在一条笔直公路一边有许多房子,现要安装消防栓,每个消防栓覆盖范围远大于房子面积,如下图所示。现求解能覆盖所有房子最少消防栓数和安装方案(问题求解过程中,可将房子和消防栓均视为直线上点)。该问题求解算法基本思路为:从左端第一栋房子开始,在其右侧m米处安装一个消防栓,去掉被该消防栓覆盖所有房子。在剩余房子中重复上述操作,直到所有房子被覆盖。算法采用设计策略为( );对应时间复杂度为(请作答此空)。

假设公路起点A坐标为0,消防栓覆盖范围(半径)为20米,10栋房子坐标为(10,20,,30,35,60,80,160,210,260,300),单位为米。根据上述算法,共需要安装( )个消防栓。以下关于该求解算法叙述中,正确是( )。

-
- A.见图A
- B.见图B
- C.见图C
- D.见图D
- 查看答案
在一条笔直公路一边有许多房子,现要安装消防栓,每个消防栓覆盖范围远大于房子面积,如下图所示。现求解能覆盖所有房子最少消防栓数和安装方案(问题求解过程中,可将房子和消防栓均视为直线上点)。该问题求解算法基本思路为:从左端第一栋房子开始,在其右侧m米处安装一个消防栓,去掉被该消防栓覆盖所有房子。在剩余房子中重复上述操作,直到所有房子被覆盖。算法采用设计策略为(请作答此空);对应时间复杂度为( )。

假设公路起点A坐标为0,消防栓覆盖范围(半径)为20米,10栋房子坐标为(10,20,,30,35,60,80,160,210,260,300),单位为米。根据上述算法,共需要安装( )个消防栓。以下关于该求解算法叙述中,正确是( )。
-
- A.分治
- B.动态规划
- C.贪心
- D.回溯
- 查看答案
阅读以下说明和流程图,填补流程图中空缺。 【说明】 设有整数数组A[1:N](N小于1),其元素有正有负。下面流程图在该数组中寻找连续排列若干个元素,使其和达到最大值,并输出其起始下标K、元素个数L以及最大和值M。 例如,若数组元素依次为3,-6,2,4,-2,3,-1,则输出K=3,L=4,M=7。该流程图中考察了A[1:N]中所有从下标i到下标j(j≥i)各元素之和S,并动态地记录其最大值M。【流程图】
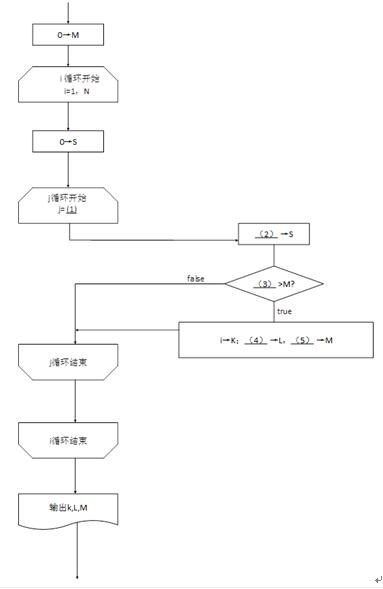
注:循环开始框内应给出循环控制变量初值和终值,默认递增值为1,格式为:循环控制变量=初值,终值
- 查看答案