阅读下列说明和C++代码,回答问题,将解答填入对应栏内。【说明】某航空公司会员积分系统将其会员划分为:普卡 (Basic)、银卡(Silver)和金卡 (Gold) 三个等级。非会员 (NonMember) 可以申请成为普卡会员。会员等级根据其一年内累积 里程数进行调整。描述会员等级调整状态图如图 5-1 所示。现采用状态 (State) 模式实现上述场景,得到如图 5-2 所示类图。
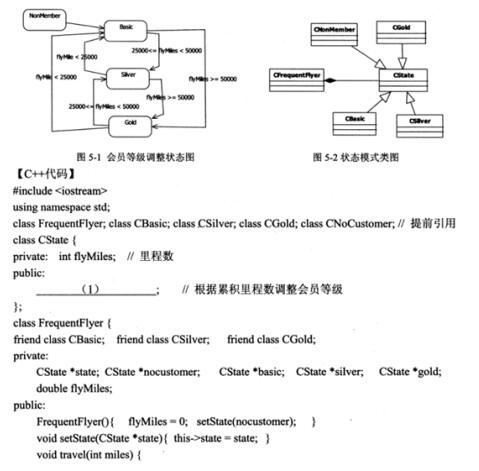

【问题1】阅读上述说明和C++代码,将应填入 (n) 处字句写在对应栏内。
正确答案及解析
正确答案
解析

你可能感兴趣的试题
在一条笔直公路一边有许多房子,现要安装消防栓,每个消防栓覆盖范围远大于房子面积,如下图所示。现求解能覆盖所有房子最少消防栓数和安装方案(问题求解过程中,可将房子和消防栓均视为直线上点)。该问题求解算法基本思路为:从左端第一栋房子开始,在其右侧m米处安装一个消防栓,去掉被该消防栓覆盖所有房子。在剩余房子中重复上述操作,直到所有房子被覆盖。算法采用设计策略为( );对应时间复杂度为( )。

假设公路起点A坐标为0,消防栓覆盖范围(半径)为20米,10栋房子坐标为(10,20,,30,35,60,80,160,210,260,300),单位为米。根据上述算法,共需要安装( )个消防栓。以下关于该求解算法叙述中,正确是(请作答此空)。
-
- A.肯定可以求得问题一个最优解
- B.可以求得问题所有最优解
- C.对有些实例,可能得不到最优解
- D.只能得到近似最优解
- 查看答案
在一条笔直公路一边有许多房子,现要安装消防栓,每个消防栓覆盖范围远大于房子面积,如下图所示。现求解能覆盖所有房子最少消防栓数和安装方案(问题求解过程中,可将房子和消防栓均视为直线上点)。该问题求解算法基本思路为:从左端第一栋房子开始,在其右侧m米处安装一个消防栓,去掉被该消防栓覆盖所有房子。在剩余房子中重复上述操作,直到所有房子被覆盖。算法采用设计策略为( );对应时间复杂度为( )。

假设公路起点A坐标为0,消防栓覆盖范围(半径)为20米,10栋房子坐标为(10,20,,30,35,60,80,160,210,260,300),单位为米。根据上述算法,共需要安装(请作答此空)个消防栓。以下关于该求解算法叙述中,正确是( )。
-
- A.4
- B.5
- C.6
- D.7
- 查看答案
在一条笔直公路一边有许多房子,现要安装消防栓,每个消防栓覆盖范围远大于房子面积,如下图所示。现求解能覆盖所有房子最少消防栓数和安装方案(问题求解过程中,可将房子和消防栓均视为直线上点)。该问题求解算法基本思路为:从左端第一栋房子开始,在其右侧m米处安装一个消防栓,去掉被该消防栓覆盖所有房子。在剩余房子中重复上述操作,直到所有房子被覆盖。算法采用设计策略为( );对应时间复杂度为(请作答此空)。

假设公路起点A坐标为0,消防栓覆盖范围(半径)为20米,10栋房子坐标为(10,20,,30,35,60,80,160,210,260,300),单位为米。根据上述算法,共需要安装( )个消防栓。以下关于该求解算法叙述中,正确是( )。

-
- A.见图A
- B.见图B
- C.见图C
- D.见图D
- 查看答案
在一条笔直公路一边有许多房子,现要安装消防栓,每个消防栓覆盖范围远大于房子面积,如下图所示。现求解能覆盖所有房子最少消防栓数和安装方案(问题求解过程中,可将房子和消防栓均视为直线上点)。该问题求解算法基本思路为:从左端第一栋房子开始,在其右侧m米处安装一个消防栓,去掉被该消防栓覆盖所有房子。在剩余房子中重复上述操作,直到所有房子被覆盖。算法采用设计策略为(请作答此空);对应时间复杂度为( )。

假设公路起点A坐标为0,消防栓覆盖范围(半径)为20米,10栋房子坐标为(10,20,,30,35,60,80,160,210,260,300),单位为米。根据上述算法,共需要安装( )个消防栓。以下关于该求解算法叙述中,正确是( )。
-
- A.分治
- B.动态规划
- C.贪心
- D.回溯
- 查看答案
阅读以下说明和流程图,填补流程图中空缺。 【说明】 设有整数数组A[1:N](N小于1),其元素有正有负。下面流程图在该数组中寻找连续排列若干个元素,使其和达到最大值,并输出其起始下标K、元素个数L以及最大和值M。 例如,若数组元素依次为3,-6,2,4,-2,3,-1,则输出K=3,L=4,M=7。该流程图中考察了A[1:N]中所有从下标i到下标j(j≥i)各元素之和S,并动态地记录其最大值M。【流程图】
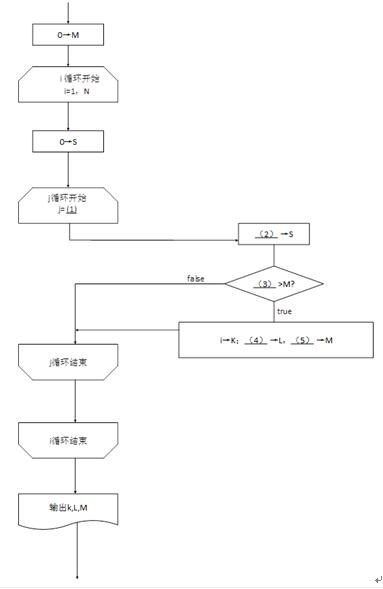
注:循环开始框内应给出循环控制变量初值和终值,默认递增值为1,格式为:循环控制变量=初值,终值
- 查看答案