快速排序是一种典型分治算法。采用快速排序对数组A[p..r]排序三个步骤如下: 分解:选择一个枢轴(pivot)元素划分数组。将数组A[p..r]划分为两个子数组(可能为空) A[p..q-1]和A[q+1..r],使得A[q]大于等于A[p..q-1]中每个元素,小于A[q+1..r]中每个元素。q值在划分过程中计算。 递归求解:通过递归调用快速排序,对子数组A[p..q-1]和A[q+1..r]分别排序。 合并:快速排序在原地排序,故不需合并操作。 【问题1】 下面是快速排序伪代码,请填补其中空缺。伪代码中主要变量说明如下: A:待排序数组 p, r:数组元素下标,从p到r q:划分位置 x:枢轴元素 i:整型变量,用于描述数组下标。下标小于或等于i元素值小于或等于枢轴元素值 j:循环控制变量,表示数组元素下标 QUICKSORT( A, p, r ){if ( p 大于 r ){q = PARTITION( A,p,r ) ;QUICKSORT( A, p, q-1 );QUICKSORT( A, q+1, r );}}PARTITION( A, p, r ){x= A[r]; i = p - 1;for( j = p ; j 大于= r - 1; j++ ){if ( A[j] 大于= x ){i = i + 1 ;交换A[i] 和 A[j];}}交换 (1) 和 (2) //注:空(1)和空(2)答案可互换,但两空全部答对方可得分return (3) } 【问题2】(1) 假设要排序包含n个元素数组,请给出在各种不同划分情况下,快速排序时间复杂度,用O记号。最佳情况为 (4)平均情况为 (5)最坏情况为 (6) (2) 假设要排序n个元素都具有相同值时,快速排序运行时间复杂度属于哪种情况? (7)(最佳、平均、最坏) 【问题3】(1) 待排序数组是否能被较均匀地划分对快速排序性能有重要影响,因此枢轴元素选取非常重要。有人提出从待排序数组元素中随机地取出一个元素作为枢轴元素,下面是随机化快速排序划分伪代码-利用原有快速排序划分操作,请填充其中空缺处。其中,RANDOM( i,j )表示随机取i到j之间一个数,包括i和j。 RANDOMIZED-PARTITION( A,p,r ){i = RANDOM( p,r );交换(8)和(9); //注:空(8)和空(9)答案可互换,但两空全部答对方可得分return PARTITION( A,p,r );} (2) 随机化快速排序是否能够消除最坏情况发生? (10)(是或否)
正确答案及解析
正确答案
解析
【问题1】(1)A[i+1] 或 A[r] (2)A[r] 或 A[i+1] (3)i+1 【问题2】(4)O(nlgn) 或 O(nlog2n) (5)O(nlgn) 或 O(nlog2n) (6)O(n2 ) (7)最坏 【问题3】(8)A[i] (9)A[r] (10)否
该题主要考查考生对分治算法快速排序理解,对伪代码、快速排序复杂度掌握,做题关键是要读懂题干,理解题干中对算法描述。 问题1考查是算法伪代码表示。分治法设计思想是将一个难以直接解决问题,分解成一些规模较小相同问题,各个击破。其快速排序算法核心处理是进行划分,根据枢轴元素值,把一个较大数组分成两个较小子数组。一个子数据组所有元素值小于等于枢轴元素值,一个子数组所有元素值大于枢轴元素值,而子数组内元素不排序。以最后一个元素为枢轴元素进行划分,从左到右依次访问数组每一个元素,与枢轴元素比较大小,并进行元素交换。在问题1给出伪代码中,当循环结束后,A[p..i]中值小于等于枢轴元素值x,而A[i+1..r-1]中值应大于x。此时A[i+1]是第一个比A[r]大元素,于是A[r]与A[i+1]交换,得到划分后两个子数组。由于划分操作(即PARTITION操作)返回枢轴元素值,因此返回值为i+1。 问题2考查是算法时间复杂度分析。当每次都能做均匀划分时,是算法最佳情况,其时间复杂度为T( N )=2T( n/2 )+O( N ),即时间复杂度为O( nlgn );算法最坏情况是每次为极不均匀划分,即长度为n数组划分后一个子数组为n-1,一个为0,其时间复杂度为T( N )=T( n-1 )+O( N ),即时间复杂度为O( n2 );算法平均情况分析起来比较复杂,假设数组每次划分为9/10:1/10,此时时间复杂度可以通过计算得到为O(nlgn);也就是说在平均情况下快速排序仍然有较好性能。问题2中假设要排序n个元素都具有相同值时,快速排序运行时间复杂度,属于最坏情况,因为每次都划分为长度为n-1和0两个子数组。 问题3中,由于随机化快速排序划分调用了PARTITION操作,而传统划分每次以数组最后一个元素作为枢轴元素。随机化快速排序消除了输入数据不同排列对算法性能影响,降低了极端不均匀划分概率,但不能保证不会导致最坏情况发生。
你可能感兴趣的试题
在一条笔直公路一边有许多房子,现要安装消防栓,每个消防栓覆盖范围远大于房子面积,如下图所示。现求解能覆盖所有房子最少消防栓数和安装方案(问题求解过程中,可将房子和消防栓均视为直线上点)。该问题求解算法基本思路为:从左端第一栋房子开始,在其右侧m米处安装一个消防栓,去掉被该消防栓覆盖所有房子。在剩余房子中重复上述操作,直到所有房子被覆盖。算法采用设计策略为( );对应时间复杂度为( )。

假设公路起点A坐标为0,消防栓覆盖范围(半径)为20米,10栋房子坐标为(10,20,,30,35,60,80,160,210,260,300),单位为米。根据上述算法,共需要安装( )个消防栓。以下关于该求解算法叙述中,正确是(请作答此空)。
-
- A.肯定可以求得问题一个最优解
- B.可以求得问题所有最优解
- C.对有些实例,可能得不到最优解
- D.只能得到近似最优解
- 查看答案
在一条笔直公路一边有许多房子,现要安装消防栓,每个消防栓覆盖范围远大于房子面积,如下图所示。现求解能覆盖所有房子最少消防栓数和安装方案(问题求解过程中,可将房子和消防栓均视为直线上点)。该问题求解算法基本思路为:从左端第一栋房子开始,在其右侧m米处安装一个消防栓,去掉被该消防栓覆盖所有房子。在剩余房子中重复上述操作,直到所有房子被覆盖。算法采用设计策略为( );对应时间复杂度为( )。

假设公路起点A坐标为0,消防栓覆盖范围(半径)为20米,10栋房子坐标为(10,20,,30,35,60,80,160,210,260,300),单位为米。根据上述算法,共需要安装(请作答此空)个消防栓。以下关于该求解算法叙述中,正确是( )。
-
- A.4
- B.5
- C.6
- D.7
- 查看答案
在一条笔直公路一边有许多房子,现要安装消防栓,每个消防栓覆盖范围远大于房子面积,如下图所示。现求解能覆盖所有房子最少消防栓数和安装方案(问题求解过程中,可将房子和消防栓均视为直线上点)。该问题求解算法基本思路为:从左端第一栋房子开始,在其右侧m米处安装一个消防栓,去掉被该消防栓覆盖所有房子。在剩余房子中重复上述操作,直到所有房子被覆盖。算法采用设计策略为( );对应时间复杂度为(请作答此空)。

假设公路起点A坐标为0,消防栓覆盖范围(半径)为20米,10栋房子坐标为(10,20,,30,35,60,80,160,210,260,300),单位为米。根据上述算法,共需要安装( )个消防栓。以下关于该求解算法叙述中,正确是( )。

-
- A.见图A
- B.见图B
- C.见图C
- D.见图D
- 查看答案
在一条笔直公路一边有许多房子,现要安装消防栓,每个消防栓覆盖范围远大于房子面积,如下图所示。现求解能覆盖所有房子最少消防栓数和安装方案(问题求解过程中,可将房子和消防栓均视为直线上点)。该问题求解算法基本思路为:从左端第一栋房子开始,在其右侧m米处安装一个消防栓,去掉被该消防栓覆盖所有房子。在剩余房子中重复上述操作,直到所有房子被覆盖。算法采用设计策略为(请作答此空);对应时间复杂度为( )。

假设公路起点A坐标为0,消防栓覆盖范围(半径)为20米,10栋房子坐标为(10,20,,30,35,60,80,160,210,260,300),单位为米。根据上述算法,共需要安装( )个消防栓。以下关于该求解算法叙述中,正确是( )。
-
- A.分治
- B.动态规划
- C.贪心
- D.回溯
- 查看答案
阅读以下说明和流程图,填补流程图中空缺。 【说明】 设有整数数组A[1:N](N小于1),其元素有正有负。下面流程图在该数组中寻找连续排列若干个元素,使其和达到最大值,并输出其起始下标K、元素个数L以及最大和值M。 例如,若数组元素依次为3,-6,2,4,-2,3,-1,则输出K=3,L=4,M=7。该流程图中考察了A[1:N]中所有从下标i到下标j(j≥i)各元素之和S,并动态地记录其最大值M。【流程图】
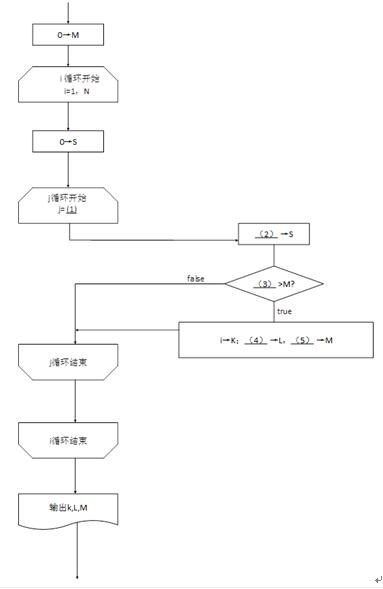
注:循环开始框内应给出循环控制变量初值和终值,默认递增值为1,格式为:循环控制变量=初值,终值
- 查看答案