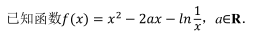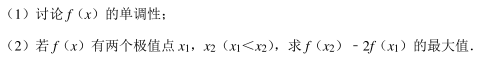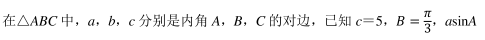已知圆 M过点(1, 0), 且与直线 x=﹣ 1 相切.
(1) 求圆心 M的轨迹 C 的方程;
(2) 过点 P(2, 0) 作直线 l 交轨迹 C 于 A、 B 两点, 点 A 关于 x 轴的对称点为 A′ ,过点 P 作 PQ⊥A′ B, 垂足为 Q, 在平面内是否存在定点 E, 使得|EQ|为定值. 若存在,求出点 E 的坐标; 若不存在, 请说明理由.
正确答案及解析
正确答案

解析
包含此试题的试卷
你可能感兴趣的试题
已知圆 M过点(1, 0), 且与直线 x=﹣ 1 相切.
(1) 求圆心 M的轨迹 C 的方程;
(2) 过点 P(2, 0) 作直线 l 交轨迹 C 于 A、 B 两点, 点 A 关于 x 轴的对称点为 A′ ,过点 P 作 PQ⊥A′ B, 垂足为 Q, 在平面内是否存在定点 E, 使得|EQ|为定值. 若存在,求出点 E 的坐标; 若不存在, 请说明理由.
- 查看答案
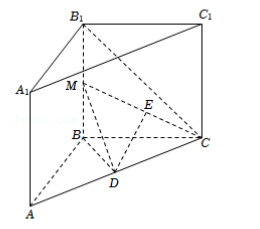
直三棱柱 ABC﹣ A 1 B 1 C 1 中, AA 1 B 1 B 为正方形, AB=BC, ∠ABC=120° , M为棱 BB 1 上任意一点, 点 D、 E 分别为 AC、 CM的中点.
(1) 求证: DE∥平面 AA 1 B 1 B;
(2) 当点 M为 BB 1 中点时, 求直线 B 1 C 和平面 CDM所成角的正弦值.
- 查看答案
从某地区高中二年级学生中随机抽取质量监测数学得分在 120 分以下和 120 分以上(含 120 分) 的学生各 250 名作为样本(全体高二学生均参加监测), 分别测出他们的注意力集中水平得分, 统计如表.
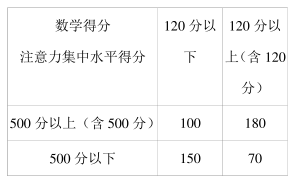
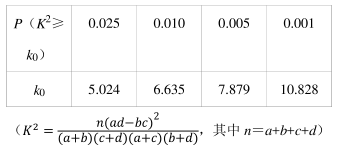
(1) 若将学生在质量监测中数学得分在 120 分以上(含 120 分). 定义为数学成绩优秀,将学生注意力集中水平得分在 500 分以上(含 500 分) 称为注意力集中水平高; 试问:能否有 99%以上的把握认为数学成绩优秀与注意力集中水平高有关?
(2) 若将上述样本的频率视为概率, 现从该地区所有高二学生中随机抽取 100 人, 设抽取到的数学得分在 120 分以上(含 120 分) 且注意力集中水平得分在 500 分以上(含 500分) 的人数为随机变量 X, 求 X的数学期望.
- 查看答案