平面内有 2n 个点(n≥2) 等分圆周, 从 2n 个点中任取 3 个, 可构成直角三角形的概率为3/11,
连接这 2n 个点可构成正多边形, 则此正多边形的边数为()
- A.6
- B.8
- C.12
- D.16
正确答案及解析
正确答案
C
解析

包含此试题的试卷
你可能感兴趣的试题
平面内有 2n 个点(n≥2) 等分圆周, 从 2n 个点中任取 3 个, 可构成直角三角形的概率为3/11,
连接这 2n 个点可构成正多边形, 则此正多边形的边数为()
-
- A.6
- B.8
- C.12
- D.16
- 查看答案

-
- A.充要条件
- B.充分不必要条件
- C.必要不充分条件
- D.既不充分也不必要条件
- 查看答案
已知全集为 U, 集合 A, B 为 U的子集, 若(∁ U A) ∩ B=∅, 则 A∩ B=()
-
- A.CUB
- B.CUA
- C.B
- D.A
- 查看答案
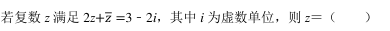
-
- A.1+2i
- B.1﹣ 2i
- C.﹣ 1+2i
- D.﹣ 1﹣ 2i
- 查看答案
已知函数 f(x) =|2x+4|﹣ |x﹣ 1|.
(1) 求不等式 f(x) >0 的解集
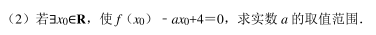
- 查看答案