已知函数 f（x） ＝x 3 +ax 2 +bx+2 在 x＝1 处取得极小值 0， 若∀x 1 ∈[m， n]， ∃x 2 ∈[m，n]， 使得 f（x 1 ） ＝f（x 2 ）， 且 x 1 ≠x 2 ， 则 n﹣ m 的最大值为（）
- A.2
- B.3
- C.4
- D.6
正确答案及解析
正确答案
C
解析
包含此试题的试卷
你可能感兴趣的试题
已知函数 f（x） ＝x 3 +ax 2 +bx+2 在 x＝1 处取得极小值 0， 若∀x 1 ∈[m， n]， ∃x 2 ∈[m，n]， 使得 f（x 1 ） ＝f（x 2 ）， 且 x 1 ≠x 2 ， 则 n﹣ m 的最大值为（）
-
- A.2
- B.3
- C.4
- D.6
- 查看答案
-
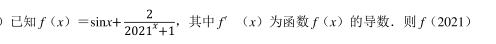
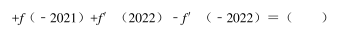
- A.0
- B.2
- C.2021
- D.2022
- 查看答案
-
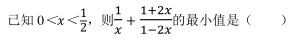
- A.5
- B.6
- C.7
- D.8
- 查看答案
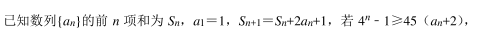则n的最小值是-
- A.4
- B.5
- C.6
- D.7
- 查看答案
已知命题 p：“∀x＞0， x+a﹣ 1≠0”， 命题 q：“∃x∈R， e x ﹣ ax＝0”， 若 p∧（￢q）为真命题， 则实数 a 的取值范围是（）
-
- A.[1， e）
- B.[0， 1]
- C.（﹣ 1， 0） ∪ [e， +∞）
- D.[e， +∞）
- 查看答案