已知命题 p：“∀x＞0， x+a﹣ 1≠0”， 命题 q：“∃x∈R， e x ﹣ ax＝0”， 若 p∧（￢q）为真命题， 则实数 a 的取值范围是（）
- A.[1， e）
- B.[0， 1]
- C.（﹣ 1， 0） ∪ [e， +∞）
- D.[e， +∞）
正确答案及解析
正确答案
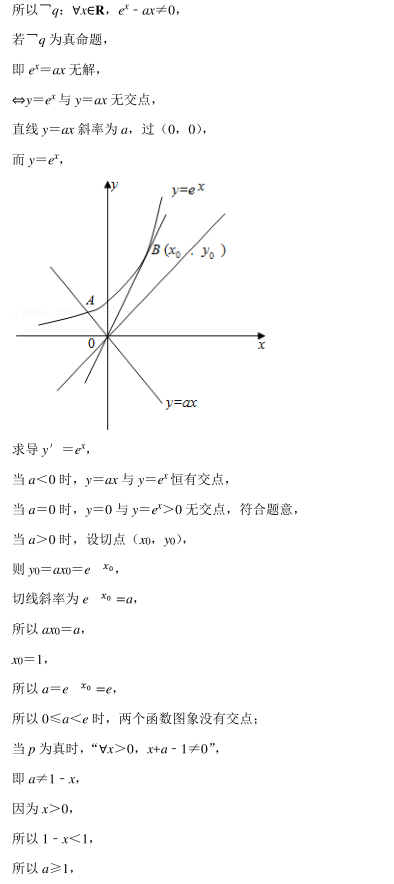
A
解析
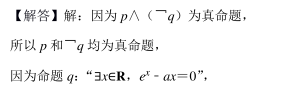
包含此试题的试卷
你可能感兴趣的试题
已知命题 p：“∀x＞0， x+a﹣ 1≠0”， 命题 q：“∃x∈R， e x ﹣ ax＝0”， 若 p∧（￢q）为真命题， 则实数 a 的取值范围是（）
-
- A.[1， e）
- B.[0， 1]
- C.（﹣ 1， 0） ∪ [e， +∞）
- D.[e， +∞）
- 查看答案
对于函数 f（x） ＝x2﹣ ax﹣ lnx（a∈R）， 下列说法正确的是（）
-
- A.函数 f（x） 有极小值， 无极大值
- B.函数 f（x） 有极大值， 无极小值
- C.函数 f（x） 既有极大值又有极小值
- D.函数 f（x） 既无极大值又无极小值
- 查看答案
已知数列{an}是等差数列， Sn为其前 n 项和
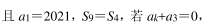则k的值为-
- A.9
- B.10
- C.11
- D.12
- 查看答案
把函数
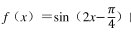的图像上所有点的横坐标伸长为原来的 2 倍， 纵坐标保持不变， 再把所得的曲线向左平移 a（a＞0） 个单位长度， 得到函数 y＝cosx 的图像，则 a 可以是（）
-
- A.A
- B.B
- C.C
- D.D
- 查看答案
-
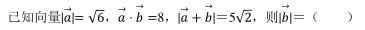
- A.2√2
- B.2√3
- C.2√7
- D.3√3
- 查看答案