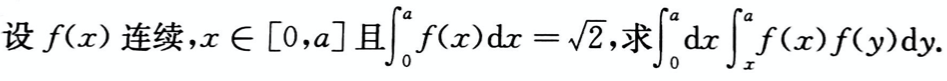设an＞0，（n＝1，2，…），Sn＝a1＋a2＋…＋an，则数列{Sn}有界是数列{an}收敛的（ ）。
- A.充分必要条件
- B.充分非必要条件
- C.必要非充分条件
- D.既非充分也非必要条件
正确答案及解析
正确答案
B
解析
由于an＞0，{Sn}是单调递增的，可知当数列{Sn}有界时，{Sn}收敛，也即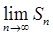
是存在的，此时有
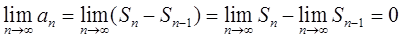
即{an}收敛。反之，{an}收敛，{Sn}却不一定有界，例如令an＝1，显然有{an}收敛，但Sn＝n是无界的。故数列{Sn}有界是数列{an}收敛的充分非必要条件，故选B项。
