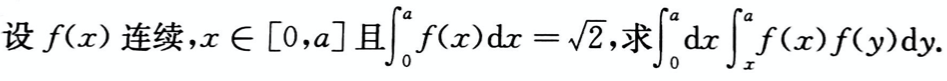设函数f(x),g(x)均有二阶连续导数,满足f(0)>0,g(0)<0,f′(0)=g′(0)=0,则函数z=f(x)g(y)在点(0,0)处取得极小值的一个充分条件是( )。
- A.f″(0)<0,g″(0)>0
- B.f″(0)<0,g″(0)<0
- C.f″(0)>0,g″(0)>0
- D.f″(0)>0,g″(0)<0
正确答案及解析
正确答案
A
解析
由z=f(x)g(y)得
?z/?x=f′(x)g(y)
?z/?y=f(x)g′(y)
B=?2z/?x?y=f′(x)g′(y)
A=?2z/?x2=f″(x)g(y)
C=?2z/?y2=f(x)g″(y)
在(0,0)点,A=f″(0)g(0),B=f′(0)g′(0)=0,C=f(0)g″(0)。由
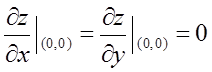
可得,(0,0)是z=f(x)g(y)可能的极值点。若z=f(x)g(y)在(0,0)有极小值。由AC-B2>0且A>0?f″(0)<0,g″(0)>0故选A项。