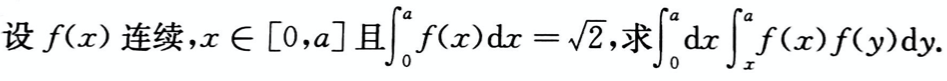设A为3阶矩阵，a1，a2为A的属于特征值1的线性无关的特征向量，a3为A的属于特征值－1的特征向量，则满足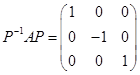
的可逆矩阵P为（ ）。
- A.（a1＋a3，a2，－a3）
- B.（a1＋a2，a2，－a3）
- C.（a1＋a3，－a3，a2）
- D.（a1＋a2，－a3，a2）
正确答案及解析
正确答案
D
解析
a1，a2是A属于特征值1的线性无关的特征向量，即Aa1＝a1，Aa2＝a2，故A（a1＋a2）＝a1＋a2，即a1＋a2也是A属于特征值1的特征向量。
设k1（a1＋a2）＋k2a2＝0，即k1a1＋（k1＋k2）a2＝0，
由于a1，a2线性无关，故k1＝k2＝0，即a1＋a2，a2线性无关。
a3是A属于特征值－1的特征向量，即Aa3＝－a3，因此A（－a3）＝－（－a3），即－a3也是A属于特征值－1的特征向量。
可取P＝（a1＋a2，－a3，a2），则P是可逆矩阵，且满足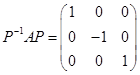
。
故应选D项。
