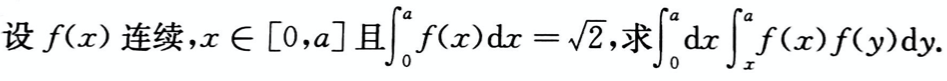设4阶矩阵A=(aij)不可逆,元素a12对应的代数余子式A12≠0,a1,a2,a3,a4为矩阵A的列向量组,A*为A的伴随矩阵,则A*x=0的通解为( )。
- A.x=k1a1+k2a2+k3a3,其中k1,k2,k3为任意常数
- B.x=k1a1+k2a2+k3a4,其中k1,k2,k3为任意常数
- C.x=k1a1+k2a3+k3a4,其中k1,k2,k3为任意常数
- D.x=k1a2+k2a3+k3a4,其中k1,k2,k3为任意常数
正确答案及解析
正确答案
C
解析
由A不可逆知,r(A)<4,又元素a12对应的代数余子式A12≠0,故r(A)≥3,从而r(A)=3。
由
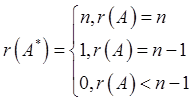
可知r(A*)=1。
故A*x=0得基础解系含有3个解向量。
因a1,a2,a3,a4为矩阵A的列向量组,则a1,a3,a4可看作A12对应矩阵列向量组的延长组,故a1,a3,a4线性无关。
又A*A=A*(a1,a2,a3,a4)=|A|E=0,故a1,a3,a4均为A*x=0的解。
综上,a1,a3,a4为A*x=0的一个基础解系,故A*x=0得通解为x=k1a1+k2a3+k3a4,其中k1,k2,k3为任意常数。
故应选C项。