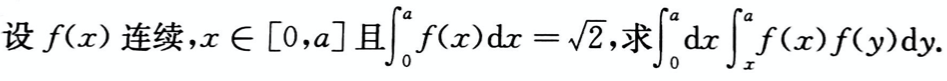设函数f（x）在区间[－2，2]上可导，且f′（x）＞f（x-名校题库网

题目详情

全站导航

首页试卷库试题库

试卷导航

学历类职业资格公务员医卫类建筑工程外语类计算机类财会类

试题导航

学历类职业资格公务员医卫类建筑工程外语类计算机类财会类

设函数f（x）在区间[－2，2]上可导，且f′（x）＞f（x）＞0，则（　　）。

因f′（x）＞f（x）＞0，f′（x）－f（x）＞0，从而e－x[f′（x）－f（x）]＞0，即[e－xf（x）]′＞0。

从而e－xf（x）在[－2，2]上单调递增，故e－0f（0）＞e1f（－1），得f（0）＞ef（－1）。

又f（x）＞0，故f（0）/f（－1）＞e，故应选B项。

由e－1f（1）＞e1f（－1），得f（1）/f（－1）＞e2，选项C错误；

由e－2f（2）＞e1f（－1），得f（2）/f（－1）＞e2，选项D错误；

对于选项A，因f′（x）＞0，故f（x）单调递增，从而f（－1）＞f（－2），得f（－2）/f（－1）＜1，选项A错误。