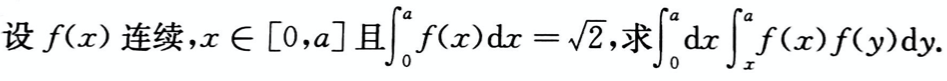设函数f(x),g(x)的2阶导函数在x=a处连续,则
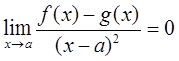
是两条曲线y=f(x),y=g(x)在x=a对应的点处相切及曲率相等的( )。
- A.充分不必要条件
- B.充分必要条件
- C.必要不充分条件
- D.既不充分也不必要条件
正确答案及解析
正确答案
A
解析
①充分性
在x=a处,由泰勒公式得
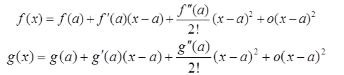
代入
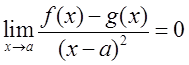
可得f(a)=g(a),f′(a)=g′(a),f″(a)=g″(a),因此两条曲线在x=a处相切且斜率相等。
②必要性
必要性不成立。例如f(x)=(x-a)2,g(x)=-(x-a)2,它们在点a相切且具有相同的曲率,但
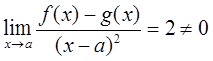
故选A。