矩阵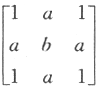
与
相似的充分必要条件为
- A.Aa=0，b=2
- B.a=0，b为任意常数
- C.a=2，b=0
- D.a=2，6为任意常数
正确答案及解析
正确答案
B
解析
两个实对称矩阵相似的充分必要条件是有相同的特征值.
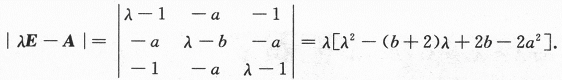
因为
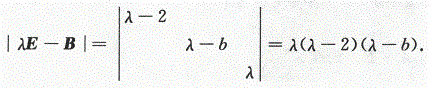
由λ=2必是A的特征值，即|2E-A|=2［2^2-2(b+2)+2b-2a^2］=0，故必有a=0.
由λ=b必是A的特征值，即|bE-A|=b［b^2-(b+2)b+2b］=0，b可为任意常数.
所以选(B).
矩阵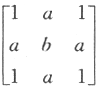与相似的充分必要条件为
两个实对称矩阵相似的充分必要条件是有相同的特征值.
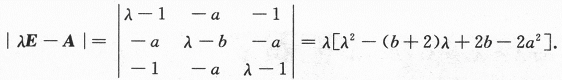
因为
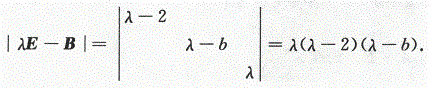
由λ=2必是A的特征值，即|2E-A|=2［2^2-2(b+2)+2b-2a^2］=0，故必有a=0.
由λ=b必是A的特征值，即|bE-A|=b［b^2-(b+2)b+2b］=0，b可为任意常数.
所以选(B).
