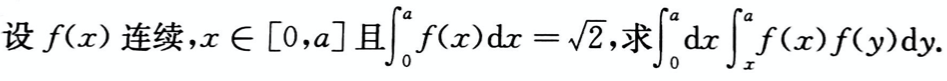设A,B,C均为n阶矩阵,若AB=C,且B可逆,则
- A.A矩阵C的行向量组与矩阵A的行向量组等价
- B.矩阵C的列向量组与矩阵A的列向量组等价
- C.矩阵C的行向量组与矩阵B的行向量组等价
- D.矩阵C的列向量组与矩阵B的列向量组等价
正确答案及解析
正确答案
B
解析
对矩阵A,C分别按列分块,记A=(α1,α2,…,αn),C=(γ,γ,…,γ). 由AB=C有
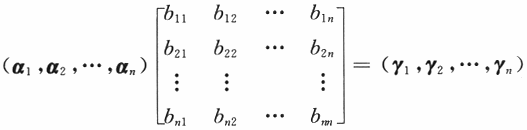
可见
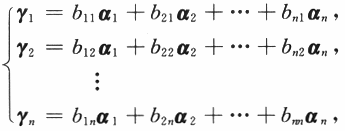
即C的列向量组可以由A的列向量组线性表出.
因为B可逆,有CB^-1=A.类似地,A的列向量组也可由C的列向量组线性表出,因此选(B).