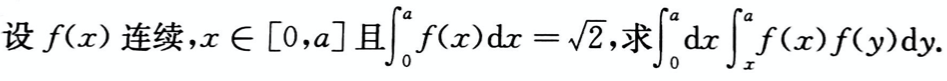曲线y=(x-1)(x-2)^2(x-3)^3(x-4)^4的拐点是
- A.A(1,0)
- B.(2,0)
- C.(3,0)
- D.(4,0)
正确答案及解析
正确答案
C
解析
(方法一)图示法:由曲线方程y=(x-1)(x-2)^2(x-3)^3(x-4)^4可知,该曲线和x轴有四个交点,即x=1,x=2,x=3,x=4,且在x=2取极大值,x=4取极小值,则拐点只能在另外两个点上,由下图不难看出(3,0)为拐点,故应选(C).
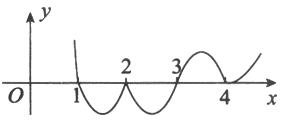
(方法二)记g(x)=(x-1)(x-2)^2(x-4)^4,则y-(x-3)^3g(x)
设g(x)在x=3处的泰勒展开式为g(x)=a0+a1(x-3)+…
则y=a0(x-3)^3+a0(x-3)^4+…
由该式可知y"(3)=0,y'"(3)=a0·3!≠0
因为a0=g(3)≠0.由拐点的第二充分条件知,(3,0)为拐点