阅读以下说明和C语言函数,将应填入 (n) 处的字旬写在答题纸的对应栏内。
【说明】
某工厂A负责为某大型企业B加工零件,A每天必须为B提供一定数量的零件。由于某种客观原因,A每天生产的零件的单价都不相同。若A某天生产的零件数多于B需要的数目,则多余的零件可以放到第二天及以后再使用,但需要收取每个零件的保管费(产品单价之外附加的费用),每个零件在不同日期收取的保管费也不相同。
例如,在5天的生产中,B要求的零件需求量及A核算出的零件单价和保管费用如表l所示:表1

A可以制订多种生产计划,但费用可能不同。例如,表2所示为生产计划及其费用。
表2
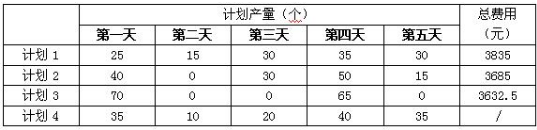
注:
(1)计划1的总费用:25*20+15*30+30*32+35*25+30*35=3835(元)
(2)计划2的总费用:40*20+15*4.5+30*32+50*25+15*5.5+15*35=3685(元)
(3)计划3的总费用:70*20+45*4.5+30*8+65*25+30*5.5=3632.5(元)
(4)计划4不可行,虽然第一天和第二天生产的零件总数比需求量多5个,但加上第三天生产的20个零件(共25个),仍不能满足B第三天的需求量(30个)。
函数find_a_plan(FILE *in)的功能是:从文件中读入若干个生产计划,从可行的计划中选出费用最小者,记录该生产计划并返回该最小费用。
全局结构体数组data[]用于保存表1所示的数据(data[0]不用),说明如下:
data[i].Qty_req: int型,表示第i天的零件需求量。
data[i].Price: double型,表示第i天生产的零件单价(元)。
data[i].Keeping_fee: double型,表示第i天保管单个零件的费用(元)。
【C语言函数】
int B_s[DAYS+1];/*记录成本最小的生产计划,B_s[0]不用,DAYS定义为天数*/
double find_a_plan(FILE *inf)
{int P_num[DAYS+l],acc_req[DAYS+1];
int i,tag = 0,acc_qty = 0;
double mincost = 1.0e20,cost_Produce,cost_Keep;
for(i=l;i<=DAYS;i++){/*到第i天时的累计零件需求量存入acc_req[i]*/ acc_qty += data[i].Qty_req;
acc_req[i] = acc_qty;
}
while(!feof(inf)){
for(i=1;i<=DAYS;i++)/*未读入一个生产计划,第i天的产量存入P_num[i]*/
if(!feof(inf))
fscanf(inf,"%d″,&P_num[i]);
tag = 0; cost_Produce = 0;cost_Keep = 0;
for(i = l, (1) ;i<=DAYS;i++){/*考察当前的生产计划*/
acc_qty +=P_num[i];/* acc_qty计录到第i天时的累计零件生产量*/
if(acc_qty<acc_req[i]){/*当前生产计划不能满足需求*/
tag = 1; break;
} /*if*/
cost_Produce += (2) ;/*计算当前生成计划的总零件价格*/
/*计算当前生成计划下的零件保管费*/
cost_Keep += ( (3) ) * data[i].Keeping_fee;
}/*for*/
if( (4) )/*若当前生产计划不可行,则继续读取下一计划*/
continue;
if( (5) )/*记录成本更小的生产计划*/
mincost = cost_Produce + cost_Keep;
for(i = 1; i <= DAYS; i++)
B_s[i] = P_num[i];
}/*if*/
}/*while*/
return mlncost;
}
正确答案及解析
正确答案
解析

你可能感兴趣的试题
【说明】
假设一个剧场有N*N个座位,顾客买票时可以提出任意有效的座号请求。下面用二维数组a[N][N]模拟剧场中的座位,a[i][j]等于0表示第i排第j列(0≤I , j≤N-1)的票尚未售出。
函数int Find ( int a[][N] , int R , int *row , int *col )的功能是:在部分票已售出的情况下,找出剧场中的R*R个空座位,要求这些座位的排列形成一个正方形。若找到满足要求的一个座位排列,则函数返回1,并算出该正方形左上角的行、列号;若未找到,返回0;
例如,一个7×7个座位的剧场如下图(a)所示,已售出部分座位的剧场如下图(b)所示,图中阴影部分表示已售出的座位,从图(b)中找出3×3正方形空座位如图(c)中斜线区所示。

函数】
int Find ( int a[][N] , int R , int *row , int *col )
{ int i,j,k,c,t; int FOUND = 0;
for ( i=0 ; !FOUND && i __(1)__ ;
while ( j for ( k=0; ___(2)___ && a[i][j+k] = = 0; k++);/* 查找第i排连续的R个空座位 */
if ( k >=R ){ /* 查找第i排连续的R个空座位 */
for ( c=0 ; c < R ; c++ ) { /* 查找其余的R*(R-1)个座位 */
for ( t = 1 ; t < R ; t++ )
if (a[ __(3)__ ] [j+c] !=0 ) break;
if ( t } /* for */
if ( ___(4)___ ) FOUND =1;
} /* if */
___(5)___ ;
} /* while */
} /* for i */
if ( FOUND ) {
*row = i-1 ; *col = j-1; /* 计算正方形区域的左上角坐标*/
return 1;
}
return 0;
}
()(15分,每空3分)
【说明】
假设一个剧场有N*N个座位,顾客买票时可以提出任意有效的座号请求。下面用二维数组a[N][N]模拟剧场中的座位,a[i][j]等于0表示第i排第j列(0≤I , j≤N-1)的票尚未售出。
函数int Find ( int a[][N] , int R , int *row , int *col )的功能是:在部分票已售出的情况下,找出剧场中的R*R个空座位,要求这些座位的排列形成一个正方形。若找到满足要求的一个座位排列,则函数返回1,并算出该正方形左上角的行、列号;若未找到,返回0;
例如,一个7×7个座位的剧场如下图(a)所示,已售出部分座位的剧场如下图(b)所示,图中阴影部分表示已售出的座位,从图(b)中找出3×3正方形空座位如图(c)中斜线区所示。

【函数】
int Find ( int a[][N] , int R , int *row , int *col )
{ int i,j,k,c,t; int FOUND = 0;
for ( i=0 ; !FOUND && i __(1)__ ;
while ( j for ( k=0; ___(2)___ && a[i][j+k] = = 0; k++);/* 查找第i排连续的R个空座位 */
if ( k >=R ){ /* 查找第i排连续的R个空座位 */
for ( c=0 ; c < R ; c++ ) { /* 查找其余的R*(R-1)个座位 */
for ( t = 1 ; t < R ; t++ )
if (a[ __(3)__ ] [j+c] !=0 ) break;
if ( t } /* for */
if ( ___(4)___ ) FOUND =1;
} /* if */
___(5)___ ;
} /* while */
} /* for i */
if ( FOUND ) {
*row = i-1 ; *col = j-1; /* 计算正方形区域的左上角坐标*/
return 1;
}
return 0;
}
- 查看答案
【说明】
一棵非空二叉树中“最左下”结点定义为:若树根的左子树为空,则树根为“最左下”结点;否则,从树根的左子树根出发,沿结点的左孩子分支向下查找,直到某个结点不存在左孩子时为止,该结点即为此二叉树的“最左下”结点。例如:下图所示的以A为根的二叉树的“最左下”结点为D,以C为根的子二叉树中的“最左下”结点为C。二叉树的结点类型定义如下:
typedef struct BSTNode {
int data ;
struct BSTNode *lch , *rch; //结点的左、右孩子指针
} *BSTree;
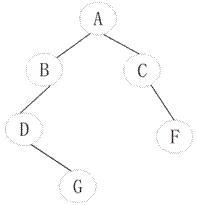
函数BSTree Find_Del (BSTree root )的功能是:若root指向一棵二茶树的根结点,则找出该结点的右子树上的“最左下”结点 *p,并从树中删除以 *p为根的子树,函数返回被删除子树的根结点指针;若该树根的右子树上不存在“最左下”结点,则返回空指针。
【函数】
BSTree Find_Del (BSTree root)
{ BSTree p, pre;
If ( !root ) return NULL; /* root 指向的二叉树为空树 */
___(1)___ ; /* 令p指向根结点的右子树 */
if ( !p ) return NULL;
___(2)___ ; /* 设置 pre 的初值 */
while ( p -> lch ) { /* 查找“最左下”结点 */
pre = p ; p = __(3)__ ;
}
if ( __(4)__ = = root ) /* root的右子树根为“最左下”结点*/
pre -> rch =NULL;
else
__(5)__ = NULL; /* 删除以“最左下”结点为根的子树*/
return p;
}
()(15分,每空3分)
【说明】
一棵非空二叉树中“最左下”结点定义为:若树根的左子树为空,则树根为“最左下”结点;否则,从树根的左子树根出发,沿结点的左孩子分支向下查找,直到某个结点不存在左孩子时为止,该结点即为此二叉树的“最左下”结点。例如:下图所示的以A为根的二叉树的“最左下”结点为D,以C为根的子二叉树中的“最左下”结点为C。二叉树的结点类型定义如下:
typedef struct BSTNode {
int data ;
struct BSTNode *lch , *rch; //结点的左、右孩子指针
} *BSTree;
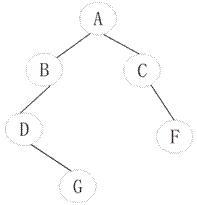
函数BSTree Find_Del (BSTree root )的功能是:若root指向一棵二茶树的根结点,则找出该结点的右子树上的“最左下”结点 *p,并从树中删除以 *p为根的子树,函数返回被删除子树的根结点指针;若该树根的右子树上不存在“最左下”结点,则返回空指针。
【函数】
BSTree Find_Del (BSTree root)
{ BSTree p, pre;
If ( !root ) return NULL; /* root 指向的二叉树为空树 */
___(1)___ ; /* 令p指向根结点的右子树 */
if ( !p ) return NULL;
___(2)___ ; /* 设置 pre 的初值 */
while ( p -> lch ) { /* 查找“最左下”结点 */
pre = p ; p = __(3)__ ;
}
if ( __(4)__ = = root ) /* root的右子树根为“最左下”结点*/
pre -> rch =NULL;
else
__(5)__ = NULL; /* 删除以“最左下”结点为根的子树*/
return p;
}
- 查看答案
阅读以下说明和C 程序,将应填入(n)处的字句写在答题纸的对应栏内。
【说明】
某旅游服务应用程序运行时,根据输入的两个城市名查找其间的距离。各城市间的距离如表4-1所示。表格中的第一行和第一列表示城市名,表中的每个元素是一个整数,代表该元素所在行和列对应的城市之间的距离(单位:km)。
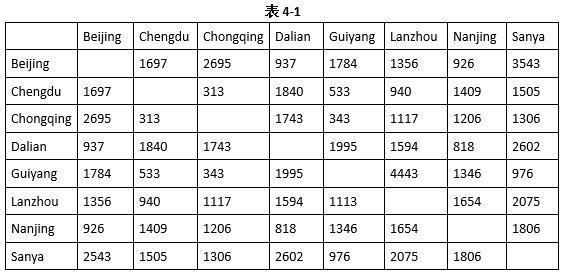
在程序中,城市名用一维全局数组cityTable存储,城市之间的距离矩阵用二维全局数组kmTable表示,并用相应的值对这两个数组进行初始化。
#define NCities 8 /* 城市个数 */
#define TRUE 1
static char * cityTable[NCities] = { /* 城市名按字典序升序排列 */
"Beijing",
...... /* 其他城市名略去 */
"Sanya",
};
static int kmTable[NCities][NCities] = {
{0, 1697, 2695, 937, 1784, 1356, 926, 2543},
{1697, 0,313, 1840,533, 940, 1409, 1505},
...... /* 剩余元素的初始值略去 */
};
程序执行时,首先按提示输入两个城市名,然后在cityTable中查找与城市名对应的下标,最后用该下标在kmTable中找到这两个城市之间的距离。
程序中定义的函数FindCityInSortedArray和GetCity说明如下:
(1)函数 FindCityInSortedArray 的功能是用二分查找法在全局数组 cityTable 中查找城市名所对应的下标值。
(2)函数GetCity的功能是读入城市名,调用函数FindCityInSortedArray来获取城市所对应的下标值。如果该城市名不存在,则提示用户重新输入。
【C 程序】
int main ( ) {
int city1,city2;
city1 = GetCity("输入第 1个城市名: ") ;
city2 = GetCity("输入第 2 个城市名: ");
printf(" %s 和%s之间的距离为:%d km.\n" ,cityTable[city1] ,
cityTable[city2] ,
kmTable[city1] [city2]);
return 0;
}
static int GetCity(char *prompt) {
char ? cityName;
int index;
cityName = (char *)malloc(20*sizeof(char));
while ( TRUE ) {
printf(" %s" ,prompt);
gets(cityName) ; /*获取输入字符串*/
index = FindCityInSortedArray(cityName);
if ( (1) ) break;
printf(" 城市名不存在,请重新输入。 \n") ;
}
free(cityName);
return (2);
}
static int FindCityInSortedArray(char*key) {
int lh ,rh ,mid ,cmp;
lh = 0;
rh = NCities - 1;
while ( (3) ) {
mid = (lh + rh) / 2;
cmp = strcmp ( (4) ); /*比较两个城市名是否相同*/
if (cmp == 0) return (5); /*两个城市名相同*/
if (cmp < 0) { rh = mid - 1; }
else { lh = mid + 1; }
}
return (-1); /*城市名不存在时返回 -1 */
}
- 查看答案
阅读以下说明和C 函数,将应填入 (n) 处的字句写在答题纸的对应栏内。
【说明】
基于管理的需要,每本正式出版的图书都有一个 ISBN 号。例如,某图书的 ISBN号为“978-7-5606-2348-1”。
ISBN 号由 13 位数字组成:前三位数字代表该出版物是图书(前缀号),中间的 9个数字分为三组,分别表示组号、出版者号和书名号,最后一个数字是校验码。其中,前缀号由国际EAN提供,已经采用的前缀号为978和979;组号用以区别出版者国家、地区或者语言区,其长度可为1~5位;出版者号为各出版者的代码,其长度与出版者的计划出书量直接相关;书名号代表该出版者该出版物的特定版次;校验码采用模10加权的算法计算得出。
校验码的计算方法如下:
第一步:前 12 位数字中的奇数位数字用 1 相乘,偶数位数字用 3 相乘(位编号从左到右依次为13到2);
第二步:将各乘积相加,求出总和S;
第三步:将总和S 除以10,得出余数R;
第四步:将10减去余数R后即为校验码V。若相减后的数值为10,则校验码为0。
例如,对于ISBN 号“978-7-5606-2348-1”,其校验码为1,计算过程为:
S=9×1+7×3+8×1+7×3+5×1+6×3+0×1+6×3+2×1+3×3+4×1+8×3=139
R = 139 mod 10 = 9
V = 10 – 9 = 1
函数check(char code[])用来检查保存在code中的一个ISBN号的校验码是否正确,若正确则返回 true,否则返回 false。例如,ISBN 号“978-7-5606-2348-1”在 code 中的存储布局如表3-1所示(书号的各组成部分之间用“-”分隔):

在函数check(char code[])中,先将13位ISBN号放在整型数组元素tarr[0]~tarr[12]中(如表3-2 所示,对应 ISBN 号的位13~位 1),由 tarr[0]~tarr[11]计算出校验码放入变量V,再进行判断。

【C 函数】
bool check(char code[ ])
{
int i,k = 0;
int S = 0 ,temp = 0;
int V ;
int tarr[13]={0};
if (strlen(code) < 17) return false;
for( i=0; i<17 ; i++ ) /*将 13位 ISBN 号存入 tarr */
if ( code [i] != '- ' )
tarr[ (1) ]= code[i] - ' 0 ';
for (i=0;(2);i++){
if( i%2 )
S += (3) ;
else
S += (4) ;
}
V = ( (5) == 0 )? 0 : 10 - S %10;
if ( tarr[12] == V)
return true ;
return false;
}
- 查看答案
阅读以下说明和C语言函数,将应填入 (n) 处的字旬写在答题纸的对应栏内。
【说明】
某工厂A负责为某大型企业B加工零件,A每天必须为B提供一定数量的零件。由于某种客观原因,A每天生产的零件的单价都不相同。若A某天生产的零件数多于B需要的数目,则多余的零件可以放到第二天及以后再使用,但需要收取每个零件的保管费(产品单价之外附加的费用),每个零件在不同日期收取的保管费也不相同。
例如,在5天的生产中,B要求的零件需求量及A核算出的零件单价和保管费用如表l所示:表1

A可以制订多种生产计划,但费用可能不同。例如,表2所示为生产计划及其费用。
表2

注:
(1)计划1的总费用:25*20+15*30+30*32+35*25+30*35=3835(元)
(2)计划2的总费用:40*20+15*4.5+30*32+50*25+15*5.5+15*35=3685(元)
(3)计划3的总费用:70*20+45*4.5+30*8+65*25+30*5.5=3632.5(元)
(4)计划4不可行,虽然第一天和第二天生产的零件总数比需求量多5个,但加上第三天生产的20个零件(共25个),仍不能满足B第三天的需求量(30个)。
函数find_a_plan(FILE *in)的功能是:从文件中读入若干个生产计划,从可行的计划中选出费用最小者,记录该生产计划并返回该最小费用。
全局结构体数组data[]用于保存表1所示的数据(data[0]不用),说明如下:
data[i].Qty_req: int型,表示第i天的零件需求量。
data[i].Price: double型,表示第i天生产的零件单价(元)。
data[i].Keeping_fee: double型,表示第i天保管单个零件的费用(元)。
【C语言函数】
int B_s[DAYS+1];/*记录成本最小的生产计划,B_s[0]不用,DAYS定义为天数*/
double find_a_plan(FILE *inf)
{int P_num[DAYS+l],acc_req[DAYS+1];
int i,tag = 0,acc_qty = 0;
double mincost = 1.0e20,cost_Produce,cost_Keep;
for(i=l;i<=DAYS;i++){/*到第i天时的累计零件需求量存入acc_req[i]*/ acc_qty += data[i].Qty_req;
acc_req[i] = acc_qty;
}
while(!feof(inf)){
for(i=1;i<=DAYS;i++)/*未读入一个生产计划,第i天的产量存入P_num[i]*/
if(!feof(inf))
fscanf(inf,"%d″,&P_num[i]);
tag = 0; cost_Produce = 0;cost_Keep = 0;
for(i = l, (1) ;i<=DAYS;i++){/*考察当前的生产计划*/
acc_qty +=P_num[i];/* acc_qty计录到第i天时的累计零件生产量*/
if(acc_qty<acc_req[i]){/*当前生产计划不能满足需求*/
tag = 1; break;
} /*if*/
cost_Produce += (2) ;/*计算当前生成计划的总零件价格*/
/*计算当前生成计划下的零件保管费*/
cost_Keep += ( (3) ) * data[i].Keeping_fee;
}/*for*/
if( (4) )/*若当前生产计划不可行,则继续读取下一计划*/
continue;
if( (5) )/*记录成本更小的生产计划*/
mincost = cost_Produce + cost_Keep;
for(i = 1; i <= DAYS; i++)
B_s[i] = P_num[i];
}/*if*/
}/*while*/
return mlncost;
}
- 查看答案