设,在x=0连续,且对任何x,y∈R有f(x﹢y)=f(x)﹢f(y)
证明:(1)f在R上连续;(2)f(x)=xf(1)。
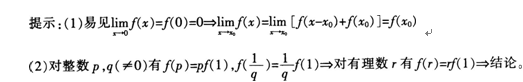
正确答案及解析
正确答案
解析
(1)因f(0) =f(0+0)=f(0) +f(0) =2f(0),所以f(0)=0。又对任意算∈(一∞,+∞)有△y=f(x+△x) -f(x) =f(x) +f(△x) -f(x) =f(△x)
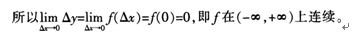
(2)先证对任意有理数r,都有以rx)=rf(x)。事实上,令y=x,得以2x)=2f(x),由数学归纳法

设,在x=0连续,且对任何x,y∈R有f(x﹢y)=f(x)﹢f(y)
证明:(1)f在R上连续;(2)f(x)=xf(1)。
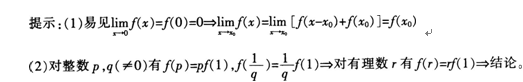
(1)因f(0) =f(0+0)=f(0) +f(0) =2f(0),所以f(0)=0。又对任意算∈(一∞,+∞)有△y=f(x+△x) -f(x) =f(x) +f(△x) -f(x) =f(△x)
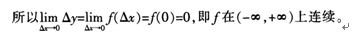
(2)先证对任意有理数r,都有以rx)=rf(x)。事实上,令y=x,得以2x)=2f(x),由数学归纳法
