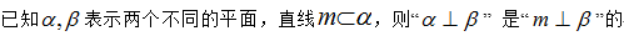
- A.充分不必要条件
- B.必要不充分条件
- C.充要条件
- D.既不充分也不必要条件
正确答案及解析
正确答案
解析
两平面垂直,那么一个平面内垂直于交线的直线垂直于另一个平面。反之,平面内一条直线垂直于另一个平面,则两平面垂直。
你可能感兴趣的试题
下面是某教师执教《不等式的运用》的教学过程。
教学的具体环节如下:
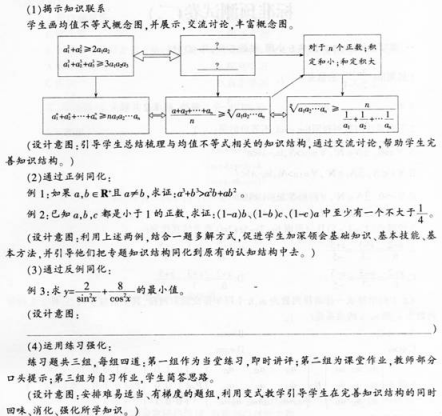
请完成下列任务:
(1)请完成概念图中问号处的不等式;(6分)
(2)请补充完例3通过反例同化的设计意图;(6分)
(3)关于《不等式的运用》的教学过程,给出你的教学目标设计;(8分)
(4)请对上述这位教师执教《不等式的运用》的教学过程作出评价。(10分)
- 查看答案
案例:
概念同化指从已有概念出发,理解并接纳新概念的过程,实质是利用演绎方式理解和掌握概念。由于数学中大多数概念是以属概念加种差的方式定义的,所以适宜采用概念同化的方式进行教学。以“奇函数,,概念教学为例简要说明概念同化的教学模式:
(1)向学生提供“奇函数”概念的定义
(2)解释定义中的词语、符号、式子所代表的含义
突出概念刻画的是:对定义域中的任意一个自变量菇,考察χ与-χ对应的函数值f(χ)与f(-χ)之间的关系以f(-χ)=-f(χ)。因此函数的定义域应该关于原点对称,满足这个条件后再考察f(-χ)=-f(χ).
(3)辨别例证,深化概念
教师向学生提供丰富的概念例证,例证中以正例为主,但也要包合适"-3的反例,尤其是一些需要考察隐含条件的例子。
(4)概念的运用
提供各种形式来运用概念,达到强化对概念的理解,促进概念体系的建构的目的,可以利用个别有一定综合性但难度不大的问题。
问题:(1)请举出反例说明(3)辨别例证,深化概念。(5分)
(2)请举例补充(4)概念的运用。(5分)
(3)请结合案例,总结出概念同化的教学模式的过程。(10分)
- 查看答案
简要论述自主学习与自学的区别。
- 查看答案
设F(χ)=f(χ)g(χ),其中函数f(χ),g(χ)在(-∞,+∞)内满足以下条件: f’(χ)=g(χ),g’(χ)=f(χ),且f(0)=0,f(χ)+g(χ)=2eχ。 (1)求F(χ)所满足的一阶微分方程; (2)求出F(χ)的表达式。
- 查看答案
袋中有l个红色球,2个黑色球与三个白球,现有放回地从袋中取两次,每次取一球,以 X,Y,Z分别表示丽次取球所取得的红球、黑球与白球的个数。
(1)求P{X=1|Z=0};
(2)求二维随机变量(X,Y)的概率分布。
- 查看答案