以“三角形的中位线定理”教学为例,简述数学定理教学的主要环节。
正确答案及解析
正确答案
解析
教学过程:
(1)情境引入
话说某天。有两个小朋友得到了一块三角形蛋糕,他们决定把它平分吃掉,你能帮他们解决这个问题吗?若又来了两个人呢?(从三角形的中线引入到三角形的中位线,可以和三角形的中线比较,加深认识。)
(2)探索新知
①学生自己动手画一条三角形的中位线,通过观察、测量,猜测三角形中位线的性质,把发现的规律用命题形式表示出来。
学生亲身经历通过观察、实验等数学活动,发现数学的过程,这对培养学生发现问题和提出问题的能力有着重要意义。
②证明三角形的中位线定理
此处证明经验较少,难度较高,可以提示学生从线段倍分转化为相等作为突破口,逐渐引导到利用平行四边形的相关知识解决问题。
③定理总结
展示三角形的中位线定理用几何语言如何表述,以及探讨定理有哪些用处。
(3)巩固练习
智力过三关如图,在△ABC 中,D,E,F 分别是 AB,AC,BC 边上的中点。
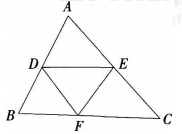
①若 BC=8cm,则 DE=__________cm。
②若△ABC 的周长为 18cm,则 ADEF 的周长为__________cm。
③图中有__________个全等三角形,有__________个平行四边形,若△ABC 的面积为 36cm
2,则△DEF 的面积为
__________cm
2。
通过三个题目练习加深对三角形中位线定理的认识,由学生表述理由可以锻炼口头表达能力。
(4)综合应用和知识拓展
①任意画一个四边形,顺次连结四边中点,得到一个什么四边形?
②证明中点四边形是一个平行四边形。
定理学习的一般环节:(1)了解定理的内容,能够解决什么问题(情境引入中体现);(2)理解定理的含义,认识定理 的条件和结论,如在公式推导过程中对条件引起注意,通过对结论从结构,功能,性质,使用步骤等角度分析以加 深印象和理解(探索新知中体现);(3)定理的证明或推导过程:学生与老师一起研究证明方法.如不需证明,学生 根据老师提供的材料体会定理规定的合理性(探索新知中体现);(4)熟悉定理的使用。循序渐进地定理的应用,将 定理纳入到已有的知识体系中去(巩固练习中体现);(5)引申和拓展定理的运用(知识拓展中体现)。