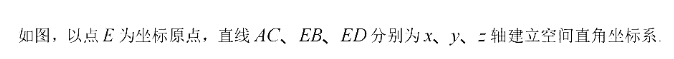题目详情
全站导航
首页 试卷 试题 资讯
试卷导航
建筑工程 职业资格 公务员 财会类 医卫类 外语类 计算机类 学历类
试题导航
建筑工程 职业资格 公务员 财会类 医卫类 外语类 计算机类 学历类

如图，四面体ABCD中AD⊥CD, AD=CD,∠ADB=∠BDC，E为AC中点.

(1)证明:平面BED⊥平面ACD:

(2) 设AB= BD=2,∠ACB=60°,点F在BD上，当△AFC的面积最小时，求CF与平面ABD所成角的正弦值.

image.png

正确答案及解析

正确答案

image.png

image.png

image.png

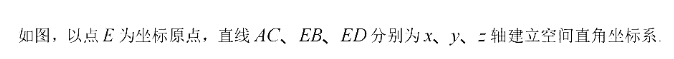
解析
暂无解析

包含此试题的试卷

你可能感兴趣的试题

问答题

如图，四面体ABCD中AD⊥CD, AD=CD,∠ADB=∠BDC，E为AC中点.

(1)证明:平面BED⊥平面ACD:

(2) 设AB= BD=2,∠ACB=60°,点F在BD上，当△AFC的面积最小时，求CF与平面ABD所成角的正弦值.

image.png

查看答案
问答题

记△ABC的内角A，B，C的对边分别为a，b，c，已知sinCsin（A-B）=sinBsin（C-A）

image.png

查看答案
填空题

image.png

image.png

查看答案
填空题

image.png

image.png

查看答案
填空题

过四点(0,0)，(4,0)， (-1,1)，(4,2)中的三 点的一个圆的方程为

查看答案

相关题库更多 +