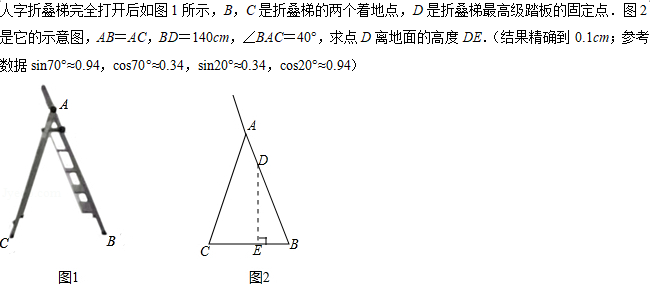
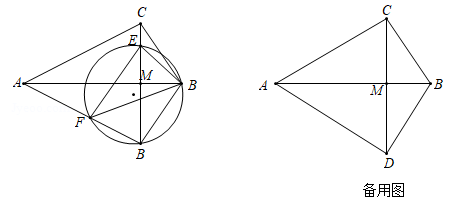
如图,在△ABC中,∠ACB=90°,将△ABC沿直线AB翻折得到△ABD,连接CD交AB于点M.E是线段CM上的点,连接BE.F是△BDE的外接圆与AD的另一个交点,连接EF,BF.
(1)求证:△BEF是直角三角形;
(2)求证:△BEF∽△BCA;
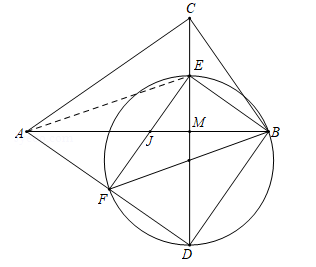
(3)当AB=6,BC=m时,在线段CM上存在点E,使得EF和AB互相平分,求m的值.
正确答案及解析
正确答案
1)证明:∵∠EFB=∠∠EDB,∠EBF=∠EDF,
∴∠EFB+∠EBF=∠EDB+∠EDF=∠ADB=90°,
∴∠BEF=90°,
∴△BEF是直角三角形.
(2)证明:∵BC=BD,
∴∠BDC=∠BCD,
∵∠EFB=∠EDB,
∴∠EFB=∠BCD,
∵AC=AD,BC=BD,
∴AB⊥CD,
∴∠AMC=90°,
∵∠BCD+∠ACD=∠ACD+∠CAB=90°,
∴∠BCD=∠CAB,
∴∠BFE=∠CAB,
∵∠ACB=∠FEB=90°,
∴△BEF∽△BCA.
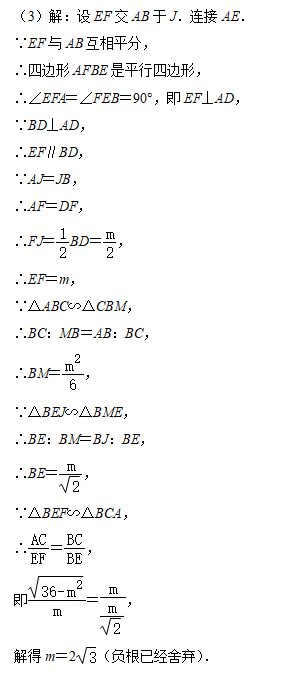
解析

包含此试题的试卷
你可能感兴趣的试题
如图,在△ABC中,∠ACB=90°,将△ABC沿直线AB翻折得到△ABD,连接CD交AB于点M.E是线段CM上的点,连接BE.F是△BDE的外接圆与AD的另一个交点,连接EF,BF.
(1)求证:△BEF是直角三角形;
(2)求证:△BEF∽△BCA;
(3)当AB=6,BC=m时,在线段CM上存在点E,使得EF和AB互相平分,求m的值.

- 查看答案
新冠疫情期间,某校开展线上教学,有“录播”和“直播”两种教学方式供学生选择其中一种.为分析该校学生线上学习情况,在接受这两种教学方式的学生中各随机抽取40人调查学习参与度,数据整理结果如表(数据分组包含左端值不包含右端值).

(1)你认为哪种教学方式学生的参与度更高?简要说明理由.
(2)从教学方式为“直播”的学生中任意抽取一位学生,估计该学生的参与度在0.8及以上的概率是多少?
(3)该校共有800名学生,选择“录播”和“直播”的人数之比为1:3,估计参与度在0.4以下的共有多少人?
- 查看答案
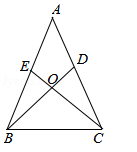
如图,已知AB=AC,AD=AE,BD和CE相交于点O.
(1)求证:△ABD≌△ACE;
(2)判断△BOC的形状,并说明理由.
- 查看答案
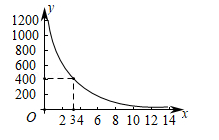
小明同学训练某种运算技能,每次训练完成相同数量的题目,各次训练题目难度相当.当训练次数不超过15次时,完成一次训练所需要的时间y(单位:秒)与训练次数x(单位:次)之间满足如图所示的反比例函数关系.完成第3次训练所需时间为400秒.
(1)求y与x之间的函数关系式;
(2)当x的值为6,8,10时,对应的函数值分别为y1,y2,y3,比较(y1﹣y2)与(y2﹣y3)的大小:y1﹣y2y2﹣y3.
- 查看答案