教学片段:
通过前面的学习,我们从几何结构特征和视图两个方面认识了空间几何体。接下来这节课我们学习空间几何体的表面积和体积。表面积是几何体表面的面积,它表示几何体表面的大小,体积是几何体所占空间的大小。好,请同学们做一做下面这道练习题。
如图,一个圆台形花盆盆口直径为20 cm,盆底直径为15 cm,盆壁长15 cm。则这个花盆的表面积是多少?(π取3.14)
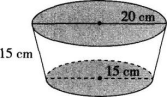
对于这道题目,教师邀请甲、乙两位同学在黑板上书写自己的解题过程,如下所示。
甲:花盆的表面积S=侧面等腰梯形的面积S1+底面圆的面积S2,即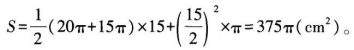
乙:花盆的表面积S=侧面扇环的面积S1+底面圆的面积S2,即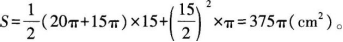
这时有学生发现,虽然甲、乙两位同学所求结果是相同的,但同学甲认为这个花盆的侧面是一个等腰梯形,乙同学认为花盆的侧面是一个扇环。
问题:
(1)请写出扇环的面积表达式及推导过程;
(2)请你分析一下,为什么甲同学会认为这个花盆的侧面是一个等腰梯形;
(3)如果你是这位教师,你接下来会怎样处理?
正确答案及解析
正确答案
解析
(1)扇环面积的表达式:s=πl(r+r’)。
推导过程:
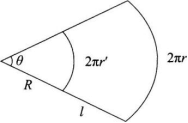
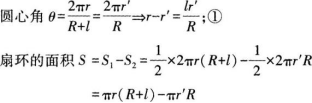
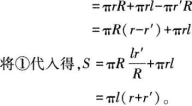
(2)甲同学认为花盆侧面是等腰梯形的原因可能有以下几点:
①对圆台的认识不足;
②空间想象能力相对薄弱;
③对问题的思考角度比较单一,思考问题不全面。
(3)如果我是这位教师,首先我会及时安抚同学们的情绪,肯定学生发现的问题,然后分别向甲、乙两名同学询问为什么侧面是等腰梯形和扇环,在甲、乙两名同学讲述的过程中,我会和学生一起分析,找出其中的误区在哪,及时订正思路,明确圆台的侧面是一个扇环,如果还有一部分学生表示不能理解,我会用圆锥的例子帮助学生理解:圆台其实就是圆锥减去其中的一个小圆锥,圆锥的侧面是一个扇形,圆台的侧面则是一个扇环
(多媒体展示分割和展开过程)。
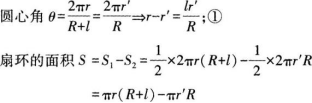
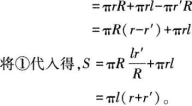
你可能感兴趣的试题
有“泥土诗人”之称的诗人是()。
-
- A.臧克家
- B.田间
- C.艾青
- D.许地山
- 查看答案
将下列各项按所表示年龄大小顺序排列,正确的顺序应是( )。
①不惑②垂髫③花甲④加冠⑤而立⑥古稀⑦半百
-
- A.②④①⑦⑤③⑥
- B.④②③⑥①⑦⑤
- C.⑥⑤③②④⑦①
- D.②④⑤①⑦③⑥
- 查看答案
明朝初年强化君主专制的措施是()。
-
- A.增设军机处
- B.采用三省六部制
- C.废除丞相.权分六部
- D.设中书省为全国最高行政机构
- 查看答案
钱穆在评论中国古代某制度时说,它“可以培植全国人民对政治之兴味……可以团结全国各地域于一个中央之统治”,这一制度是()。
-
- A.郡县制
- B.察举制
- C.科举制
- D.行省制
- 查看答案
1931年,一位给人们带来光明的科学家重病的消息牵动着世界人民的心,几十名记者为他守夜。每隔一个小时就对外发布一次消息:“灯”还亮着。这位科学家是( )。
-
- A.瓦特
- B.法拉第
- C.爱迪生
- D.爱因斯坦
- 查看答案