针对“正弦定理”的教学，教师制定了如下的教学目标：
①通过对任意三角形边长和角度关系的探索，掌握正弦定理的内容及其证明方法；
②会用正弦定理解决与实际生活有关的问题。
依据这一教学目标，请完成下列任务：
（1）设计一个探索正弦定理的教学片段，并说明设计意图：
（2）设计一个习题（不必解答），以帮助学生理解该定理，并说明设计意图：
（3）设计一个实例，体会正弦定理在生活中的应用，并说明设计意图。
正确答案及解析
正确答案
解析
（1）探究环节
提出问题：我们知道，在任意三角形中有大边对大角，小边对小角的边角关系。我们能否得到这个边角关系准确量化的表示呢?
探究一：直角三角形中边与角的关系
教师给出直角三角形图形，以及角和边长的表示，即在Rt△ABC中，∠c为直角，∠A，∠B，∠C所对的边长分别为a，b，c。
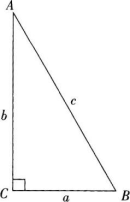
问题：由锐角三角函数的定义，你能写出sinA与sinB的关系吗?
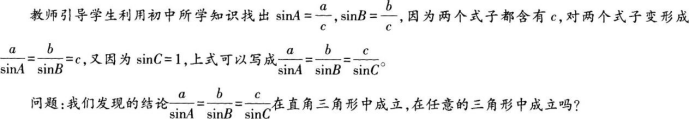
教师引导学生分两种情况（锐角三角形和钝角三角形），然后按照化未知为已知的思路，构造直角三角形。
探究二：锐角三角形中的边角关系
教师给出任意锐角三角形图形，出示已知条件及问题。
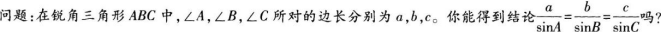
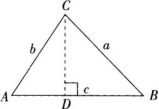
从而证得此结论在锐角三角形中也成立。
问题：当三角形是钝角三角形时，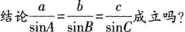
延用上述方法，学生自己进行证明操作，全班交流证明过程，教师巡视指导。
教师总结：通过上面的探索我们发现任意三角形中存在结论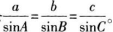
教师给出正弦定理的定义，并强调对任意三角形都存在此定理。
（2）习题：
在三角形ABC中，已知a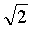=2
，b=2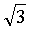
，∠A=45°，解三角形。
【设计意图】让学生用正弦定理解题，感受到应用该定理的简便之处，题目隐含两种结果，考查了学生对已学知识的掌握程度，帮助学生加深对解三角形这类题目的理解。
（3）A，B两村庄在河的两岸，有一工程队，要在A，B两村庄建一座大桥，要测量两点之间的距离，测量者在A村的同侧，在所在河岸边选定一点C，测出AC之间的距离是55米，∠ACB=60°，∠BAC=45°，求AB之同的距离。
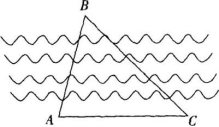
【设计意图】让学生认识到正弦定理在生活中的应用，激发其学习兴趣，增强其自信心。
你可能感兴趣的试题
《义务教育数学课程标准（2011年版）》强调，课程内容要反映社会的需要、数学的特点，要符合学生的认知规律。课程内容的组织要重视过程，处理好（）的关系。
-
- A.预设与生成
- B.抽象与具体
- C.数学与实际生活
- D.过程与结果
- 查看答案
设α是某一方程组的解向量，k为某一常数，则kα也为该方程组的解向量。（ ）
- 查看答案
-
- A.0
- B.1
- C.2
- D.3
- 查看答案
案例：
在有理数运算的课堂教学片段中，某学生的板演如下：
针对该学生的解答，教师进行了如下教学：
师：请仔细检查你的演算过程，看是否正确无误？
生：好像正确吧。
请分析例题1、例题2中每一步运算的依据。（10分）
- 查看答案
初中数学课程是一门国家课程，其主要内容包括课程目标、教学内容、教学过程和( )等
-
- A.评价手段
- B.教学方法
- C.教学手段
- D.教学实践
- 查看答案