在“三角形全等的判定”的复习课中，教师做了如下的准备：例如：-名校题库网

题目详情

全站导航

首页试卷试题资讯

试卷导航

建筑工程职业资格公务员财会类医卫类外语类计算机类学历类

试题导航

建筑工程职业资格公务员财会类医卫类外语类计算机类学历类

在“三角形全等的判定”的复习课中，教师做了如下的准备：

例如：如图1，AB=AC，E，F分别是AB，AC的中点，求证：△ABF≌△ACE。

中学数学学科知识与教学能力,章节练习,基础复习,初级中学练习

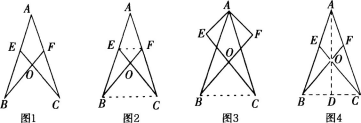
课堂设计是让学生利用SAS证明这个结论后进行下面的变式训练：

（1）改变E，F在AB，AC上的位置，如果让上述结论仍然成立，需要满足什么条件?

（2）在（1）成立的条件下连结BC，EF，让学生寻找全等三角形（记BF，CE的交点为O），让学生证明△BOE≌△COF，为以后学习ASA埋下伏笔（如图2）。

在实际教学过程中并没有按照教师的设计方向发展。当连结BC后，学生顺利地证明出△ABF≌△ACE及△BCE≌△CBF，教师要求学生仿照上面的方法，对图形稍作变化，编一道几何题。话音刚落，一名学生就举手发言：“把△ACE绕着A点旋转一定的角度（如图3），原来的结论成立吗?”

另外一名学生接着说：“作射线AO交BC边于点D，则射线AO平分∠BAC，请找出图中全等的三角形（如图4）。”

学生的想法已经偏离了教师的预设，但还是围绕着三角形的判定及运用，于是教师顺水推舟，问：“谁能告诉大家为什么AO平分∠BAC?”在教师引导下，学生的思维更加活跃，马上有学生回答：“因为△BCE≌△CBF，所以∠OCB=∠OBC，进而OB=OC，利用SAS有△ABO≌△ACO，从而有∠BAO=∠CAO。”另一位学生接着说：“可以用SSS来证明△ABO≌△ACO……”“老师，还能用SAS证明△AEO≌△AFO。”一节课就在热烈的讨论中结束了。

问题：

（1）对上述教学过程进行评价；（15分）

（2）简要说明预设与生成的关系。（5分）

正确答案及解析

正确答案

解析

（1）案例中的教学过程突破了教师的预设，将预设的“知识变式练习”变成了探究两个学生提出的问题，进而获得新知识的过程。这样做让教师的预设落了空——没有完成知识运用的目标，不过师生却发现了知识之间新的联系，尤其是学生在这个过程中获得的知识经验，会成为他们学习更为抽象、深刻和系统的文化科学知识的重要基础。这就是课堂教学具有的生成性特征，它使得每一次教学都成为唯一，不可复制。苏霍姆林斯基说过：“教育的技巧并不在于能预见到课堂的所有细节，而是在于根据当时的具体情况，巧妙地在学生不知不觉中做出相应的变动。”

（2）预设与生成是辩证的对立统一体，课堂教学既需要预设，也需要生成，预设与生成是课堂教学的两翼，缺一不可。预设体现对文本的尊重，生成体现对学生的尊重；预设体现教学的计划性和封闭性，生成体现教学的动态性和开放性，两者具有互补性。教学既要重视知识学习的逻辑和效率，又要注重生命体验的过程和质量。为此，要认真处理预设与生成的关系，使两者相辅相成、相互促进。