
正确答案及解析
正确答案
解析
(Ⅰ)相似的矩阵有相同的特征值,因此特征值之和相同,又因为矩阵特征值之和等于矩阵的迹(矩阵对角线元素之和),所以有Σaii=Σbii,|A|=|B|,即
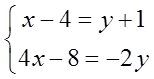
求解得到x=3,y=-2。
(Ⅱ)矩阵B的特征多项式f(λ)=|λE-B|=(λ-2)(λ+1)(λ+2),因此B的特征值为2,-1,-2。A与B相似,因此A的特征值也为2,-1,-2。
下面分别求A和B的特征向量:



(Ⅰ)相似的矩阵有相同的特征值,因此特征值之和相同,又因为矩阵特征值之和等于矩阵的迹(矩阵对角线元素之和),所以有Σaii=Σbii,|A|=|B|,即
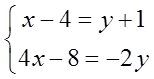
求解得到x=3,y=-2。
(Ⅱ)矩阵B的特征多项式f(λ)=|λE-B|=(λ-2)(λ+1)(λ+2),因此B的特征值为2,-1,-2。A与B相似,因此A的特征值也为2,-1,-2。
下面分别求A和B的特征向量:

