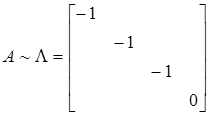设A为4阶实对称矩阵,且A2+A=O。若A的秩为3,则A相似于( )。
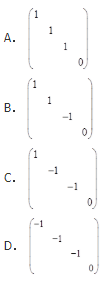
- A.见图A
- B.见图B
- C.见图C
- D.见图D
正确答案及解析
正确答案
D
解析
设λ为A的特征值,由于A2+A=O,所以λ2+λ=0,即(λ+1)λ=0。这样A的特征值为-1或0。由于A为实对称矩阵,故A可相似对角化,即A~Λ,r(A)=r(Λ)=3。
因此
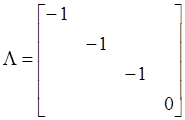
即
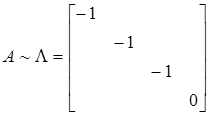
设A为4阶实对称矩阵,且A2+A=O。若A的秩为3,则A相似于( )。

设λ为A的特征值,由于A2+A=O,所以λ2+λ=0,即(λ+1)λ=0。这样A的特征值为-1或0。由于A为实对称矩阵,故A可相似对角化,即A~Λ,r(A)=r(Λ)=3。
因此
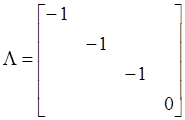
即