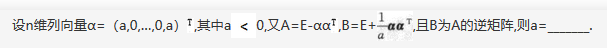已知函数f(x，y)=x+y+xy，曲线C：x^2+y^2+xy=3，求f(x，y)在曲线C上的最大方向导数.
正确答案及解析
正确答案
解析
【分析】函数在一点处沿梯度方向的方向导数最大，进而转化为条件最值问题
函数f(x，y)=x+y+xy在点(x，y)处的最大方向导数为
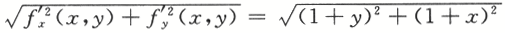
构造拉格朗日函数
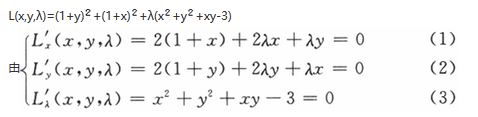
(2)-(1)得(y-x)(2+λ)=0
若y=x，则y=x=±1，若λ=-2，则x=-1，y=2或x=2，y=-1.
把两个点坐标代入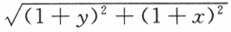
中，f(x，y)在曲线C上的最大方向导数为3.
【评注】此题有一定新意，关键是转化为求条件极值问题.
包含此试题的试卷
你可能感兴趣的试题
在社会规范学习与道德品质发展的研究中，班都拉（ABandura)等心理学家的研究重点是
-
- A.道德认识
- B.道德情感
- C.道德意志
- D.道德行为
- 查看答案
