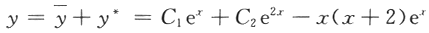求微分方程y"-3y'+2y=2xe^x的通解.
正确答案及解析
正确答案
解析
【解】由方程y-3y'+2y=0的特征方程解得特征根,所以方程y-3y'+2y=0的通解为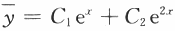
设y-3y'+2y=2xe^x的特解为y^*=x(ax+b)e^x,则(y^*)'=(ax^2+2ax+bx+b)e^x(y^*)=(ax^2+4ax+bx+2a+2b)e^x
代入原方程,解得a=-1,b=-2,故特解为:y^*=x(-x-2)e^x,所以原方程的通解为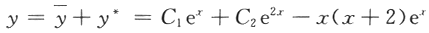
求微分方程y"-3y'+2y=2xe^x的通解.
【解】由方程y-3y'+2y=0的特征方程解得特征根,所以方程y-3y'+2y=0的通解为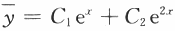
设y-3y'+2y=2xe^x的特解为y^*=x(ax+b)e^x,则(y^*)'=(ax^2+2ax+bx+b)e^x(y^*)=(ax^2+4ax+bx+2a+2b)e^x
代入原方程,解得a=-1,b=-2,故特解为:y^*=x(-x-2)e^x,所以原方程的通解为