设A为四阶实对称矩阵，且A^2+A=O.若A的秩为3，则A相似于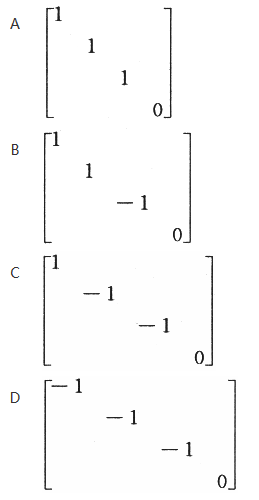
- A.见图A
- B.见图B
- C.见图C
- D.见图D
正确答案及解析
正确答案
D
解析
这是一道常见的基础题，由Aα=λα，α≠0知A^nα=λ^nα，那么对于A^2+A=0
(λ^2+λ)α=0
λ^2+λ=0所以A的特征值只能是0或-1再由A是实对称必有A～A，而A即是A的特征值，那么由r(A)=3，可知(D)正确
设A为四阶实对称矩阵，且A^2+A=O.若A的秩为3，则A相似于
这是一道常见的基础题，由Aα=λα，α≠0知A^nα=λ^nα，那么对于A^2+A=0(λ^2+λ)α=0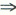λ^2+λ=0所以A的特征值只能是0或-1再由A是实对称必有A～A，而A即是A的特征值，那么由r(A)=3，可知(D)正确
