已知微分方程y’+y=f(x),其中f(x)是R上的连续函数.
(Ⅰ)若f(x)=x,求方程的通解.
(Ⅱ)若f(x)是周期为T的函数,证明:方程存在唯一的以T为周期的解.
正确答案及解析
正确答案
解析
【解】(Ⅰ)若f(x)=x,则方程为y'+y=x通解为
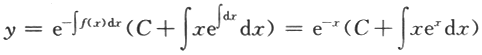
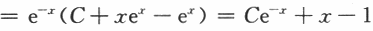
(Ⅱ)设y(x)为方程的任意解,则y'(x+T)+y(x+T)=f(x+T).
而f(x)周期为T,有f(x+T)=f(x).又y'(x)+y(x)=f(x).
因此y'(x+T)+y(x+T)-y'(x)-y(x)=0,有(e^x[y(x+T)-y(x)])'=0,
即e^x[y(x+T)=y(x)]=C.取C=0得y(x+T)-y(x)=0,
y(x)为唯一以T为周期的解.
包含此试题的试卷
你可能感兴趣的试题

-
- A.1.7
- B.1.9
- C.2.1
- D.2.0
- 查看答案

-
- A.0. 60
- B.0.50
- C.0. 12
- D.0.20
- 查看答案
如何理解今年一季度经常账户逆差的原因和影响?
- 查看答案
M 公司是一个无负债公司,其每年预期税息前收益为 10000 元,股东要求的 权益回报率为 16%,M 公司所得税率为 35%,但没有个人所得税,设所有交易 都在完善的资本市场中运行,问: A.M 公司的价值为多少? B.如果 M 公司借入面值为无负债公司价值的一半的利率为 10%的债务,债务 没有风险,并且所筹集的债务资金全部用于赎回股权,则此时公司的价值变为多 少?而权益资本成本为多少
- 查看答案
中美贸易失衡的原因并评价特朗普的贸易政策?
- 查看答案