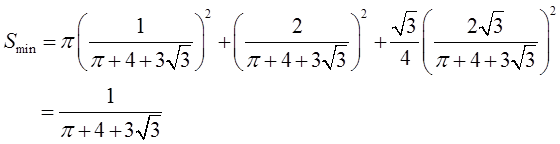将长为2m的钢丝分为三段,依次围成成圆、正方形和正三角形,三个图形的面积之和是否存在最小值若存在,求出最小值。
正确答案及解析
正确答案
解析
设圆的半径为x,正方形边长为y,正三角形边长为z,则有:2πx+4y+3z=2,其中x≥0,y≥0,z≥0。
三个图形面积之和为
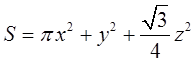
利用拉格朗日数乘法,建拉格朗日函数
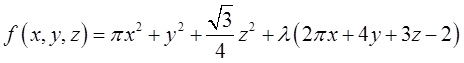
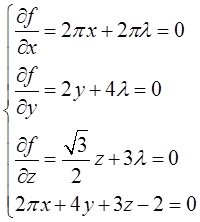
求解上述方程得到,驻点为
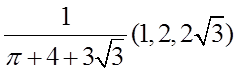
此时三个图形总面积最小,最小面积为
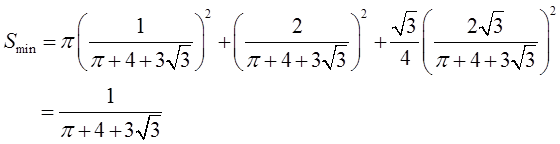
将长为2m的钢丝分为三段,依次围成成圆、正方形和正三角形,三个图形的面积之和是否存在最小值若存在,求出最小值。
设圆的半径为x,正方形边长为y,正三角形边长为z,则有:2πx+4y+3z=2,其中x≥0,y≥0,z≥0。
三个图形面积之和为
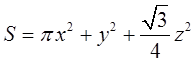
利用拉格朗日数乘法,建拉格朗日函数
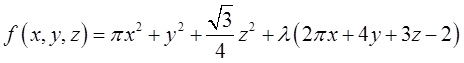
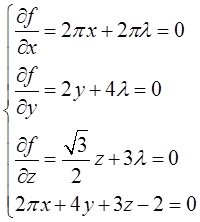
求解上述方程得到,驻点为
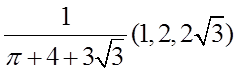
此时三个图形总面积最小,最小面积为