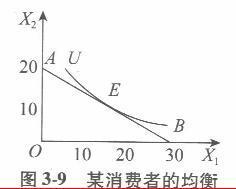
假设某消费者的均衡如图3-9所示。其中,横轴OX1和纵轴OX2分别表示商品1和商品2的数量,线段AB为消费者的预算线,曲线U为消费者的无差异曲线,E点为效用最大化的均衡点。已知商品1的价格P1=2元。
(1)求消费者的收入。 (2)求商品2的价格P2。 (3)写出预算线方程。 (4)求预算线的斜率。 (5)求E点的MRS12的值。
正确答案及解析
正确答案
解析
(1)图3-9中的横截距表示消费者的收入全部购买商品1时可购买30单位,又已知P.=2元,则消费者的收入M=2 x30 =60元。 (2)图3-9中的纵截距表示消费者的收入全部购买商品2时可购买20单位,由(1)已知收人M =60元,所以商品2的价格P2=M/20=60/20=3元。 (3)已知预算线方程的一般形式为P1x1+P2x2=M。所以,由(1)、(2)可将预算线方程具体写为2x1+3x2= 60。 (4)将(3)中的预算线方程进一步整理为X2=-2/3X, +20。很清楚,预算线的斜率为-2/3。 (5)茌消费者效用最大化的均衡点E上有MRS12=P1/P2,即无差异曲线的斜率的绝对值MRS等于预算线的斜率的绝对值2。因此,MRS12=P1/P2=2/3