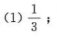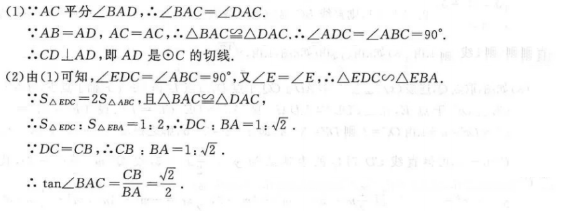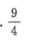∴直线AM的解析式为y=2x-4.
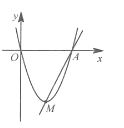
" data-timutype="tian" data-ci="0" data-orderid="2">如图,已知经过原点的抛物线y=2x²+mx与x轴交于另一点A(2,0).
(1)求m的值和抛物线顶点M的坐标;
(2)求直线AM的解析式.
- 参考答案:
解(1)∵抛物线y=2x²+mx过点A(2,0),
∴2×2²+2m=0,解得m=-4,
∴y=2x²-4x,
∴y=2(x—1)²—2
∴顶点M的坐标是(1,-2).
(2)设直线AM的解析式为y=kx+b(k≠0),
∵图象过A(2,0),M(1,-2),

∴直线AM的解析式为y=2x-4.
- 您的答案:
参考解析:
∴这一周四个小组所有成员平均每人参与活动的时间是2.6小时
" data-timutype="tian" data-ci="0" data-orderid="3">为了更好地了解党的历史,宣传党的知识,传颂英雄事迹,某校团支部组建了;A.党史宜讲;B.歌曲演唱;C.校刊编撰;D.诗歌创作等四个小组,团支部将各组人数情况制成了如下统计图表(不完整).

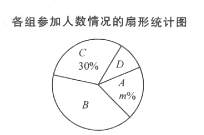
根据统计图表中的信息,解答下列问题;
(1)求a和m的值;
(2)求扇形统计图中D所对应的圆心角度数;
(3)若在某一周各小组平均每人参与活动的时间如下表所示:

求这一周四个小组所有成员平均每人参与活动的时间.
- 参考答案:
(1)由题意可知四个小组所有成员总人数是15÷30%=50(人)
∴a-50一10一15一5-20,
m%=10÷50X100%=20%
∴m=20
(2)
∵5÷50×360°=36°
∴扇形统计图中D所对应的圆心角度数是36°
(3)
∴这一周四个小组所有成员平均每人参与活动的时间是2.6小时
- 您的答案:
参考解析:
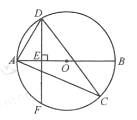
如图,已知AB是OO的直径,∠ACD是⌒AD所对的圆周角,∠ACD=30°
(1)求∠DAB的度数;
(2)过点D作DE上AB,垂足为E,DE的延长线交⊙O于点F.
若AB=4,求DF的长.
今年以来,我市接待的游客人数逐月增加﹐据统计,游玩某景区的游客人数三月份为4万人,五月份为5.76万人.
(1)求四月和五月这两个月中,该景区游客人数平均每月增长百分之几;(2)若该景区仅有A,B两个景点,售票处出示的三种购票方式如下表所示:

据预测,六月份选择甲,乙,丙三种购票方式的人数分别有2万,3万和2万.并且当甲、乙两种门票价格不变时,丙种门票价格每下降1元,将有600人原计划购买甲种门票的游客和400人原计划购买乙种门票的游客改为购买丙种门票.
①若丙种门票价格下降10元,求景区六月份的门票总收人;
②问:将丙种门票价格下降多少元时,景区六月份的门票总收入有最大值?最大值是多少万元?

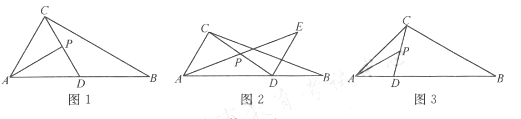
已知在△ACD中,P是CD的中点;B是AD延长线上的一点,连结BC,AP.
(1)如图1,若∠ACB=90°,∠CAD=60°,BD=AC,AP=√3 ,求BC的长.
(2)过点D作DE//AC,交AP延长线于点E,如图2所示.若∠CAD=60°,BD=AC,
求证:BC=2AP.
(3)如图3,若∠CAD=45°,是否存在实数m,当BD=mAC时,BC=2AP?若存在,请直
接写出m的值;若不存在,请说明理由.
某矩形人行道由相同的灰色正方形地砖与相同的白色等媵直角三角形她砖排列而成,图1表示此人行道的地砖排列方式,其中正方形地砖为连续排列. .
[观察思考]:
当正方形地砖只有1块时,等腰直角三角形地砖有6块(如图2);当正方形坛砖有2块时,等腰直角三角形地砖有8块(如图3);以此类推

[规律总结]
(1)若人行道上每增加1块正方形地砖,则等腰直角三角形地砖增加___块
(2)若一条这样的人行道一共有n (n 为正整数)块正方形地砖,则等腰直角三角形地砖的块数为___(用含n的代数式表示)
[问题解决].
(3)现有 2021块等腰直角三角形地砖,若按此规律再注一条人行道,要求等腰直角三角形地砖剩余最少,则需要正方形增砖多少块?
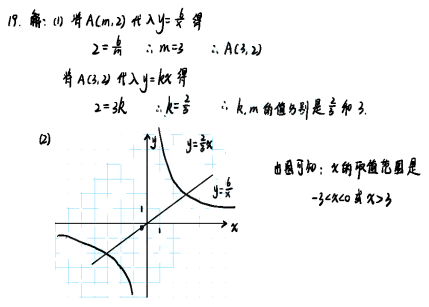
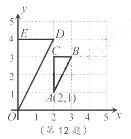
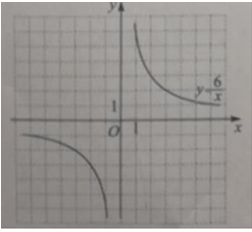
己知正比例函数y=kx(k≠0)与反比例函数y=6/x的图象都经过点A(m,2)
(1)求k,m的值
(2)在图中画出正比例函散y=kx的图象,并根据图象,写出正比例函数值大于反比例函数值时x的取值范围
如图,圆О中两保豆相垂直的弦AB。CD交于点E
(1)M是CD的中点,OM=3,CD=12,求圆О的半径长;
(2)点F在 CD 上,且 CE=EF,求证:AF⊥BD

为了解全市居民用户用电情况,莱部门从居民用户中随机抽取100户进行月用电量(单位:kW·h)调查,按月用电量50~100,100~-150,150~-200,200~250,250~300,300~350进行分组,绘制频数分布直方图如下
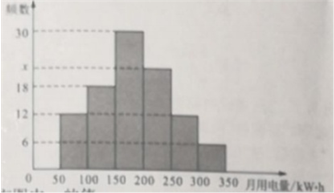
(1)求频数分布直方图中x的值
(2)判断这100户居民用户月用电量数据的中位数在哪一组(直接写出结果);
(3)设各组居民用户月平均用电量如表

己知抛物线y=ax²-2x+l (a≠0)的对称轴为直线x=1
(1)求a的值;
(2)若点M(x1,y1),N(x2,y2)都在此抛物线上,且- 1<x1<0,1<x2<2.比较y1与y2的大小,并说明理由;
(3)设直线y=m(m>0)与抛物线y=ax²-2x+l交于点A、B,与抛物线y=3(x - 1)²交于点C,D,求线段AB与线段CD的长度之比

为了参加全市中学生“党史知识竞赛”,某校准备从甲,乙2名女生和丙、丁2名男生中任选2人代表学校参加比赛.
(1)如果已经确定女生甲参加,再从其余的候选人中随机选取1人,则女生乙被选中的概率是_;
(2)求所选代表恰好为1名女生和1名男生的概率
为了做好防疫工作,学校准备购进一批消毒液.已知2瓶A型消毒液和3瓶B型消毒液共需41元,5瓶A型消毒液和2瓶B型消毒液共需53元.
(1)这两种消毒液的单价各是多少元?
(2)学校准备购进这两种消毒液共90瓶,且B型消毒液的数量不少于A型消毒液数量的⅓,请设计出最省钱的购买方案,并求出最少费用
如图,Rt△ABC 中,∠ABC=90°,以点C为圆心,CB为半径作⊙C,D为OC上一点,连接AD.CD ,AB=AD ,AC平分∠BAD.
(1)求证:AD是⊙C的切线;
(2)延长AD、BC相交于点E,若S△EDC=2S△ABC,求tan∠BAC的值.
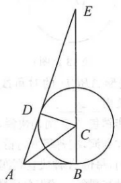
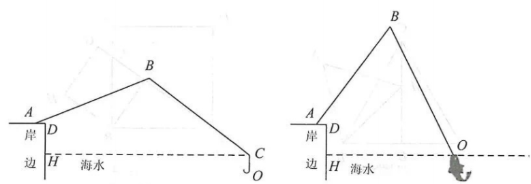
我市的前三岛是众多海钓人的梦想之地.小明的爸爸周末去前三岛钓鱼,将鱼竿AB摆成如图1所示.已知AB=4.8 m,鱼竿尾端A离岸边0.4 m,即 AD=0.4 m.海面与地面AD平行且相距1.2 m,即DH=1.2 m.
(1)如图1,在无鱼上钩时,海面上方的鱼线BC与海面HC 的夹角∠BCH=37°,海面下方的鱼线CO与海面HC垂直,鱼竿AB与地面AD的夹角∠BAD=22°.求点О到岸边DH的距离;
(2)如图2,在有鱼上钩时,鱼竿与地面的夹角LBAD=53°,此时鱼线被拉直,鱼线BO=5.46 m,点О恰好位于海面.求点О到岸边DH的距离.
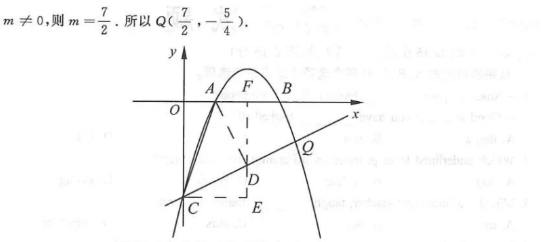
如图,抛物线y=mx²+(m²+3)x-(6m+9)与x轴交于点A,B,与y轴交于点C,已知B(3,0)
(1)求m的值和直线BC对应的函数表达式;
(2)P为抛物线上一点,若S△PBC=S△ABC,请直接写出点P的坐标;
(3)Q为抛物线上一点,若∠ACQ=45°,求点Q的坐标.
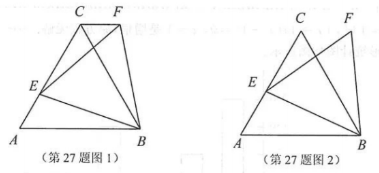
在数学兴趣小组活动中,小亮进行数学探究活动.
(1)△ABC是边长为3的等边三角形,E是边AC上的一点,且AE=1,小亮以BE为边作等边三角形BEF,如图1.求 CF的长;
(2)△ABC是边长为3的等边三角形,E是边AC上的一个动点,小亮以BE为边作等边三角形BEF,如图⒉在点E从点C到点A 的运动过程中,求点F所经过的路径长;
(3)△ABC是边长为3的等边三角形,M是高CD 上的一个动点,小亮以BM为边作等边三角形BMN,如图3.在点M从点C到点D的运动过程中,求点Ⅳ所经过的路径长;
(4)正方形ABCD的边长为3,E是边CB上的一个动点,在点E从点C到点B的运动过程中,小亮以B为顶点作正方形BFGH ,其中点F,G都在直线AE上,如图4.当点E到达点B时,点F、G,H 与点B重合.则点H所经过的路径长为_▲_,点G所经过的路径长为_▲.
小敏和小霞两位同学解方程3(x-3)=(x-3)²的过程如下框:

你认为他们的解法是否正确?若正确请在框内打“√”若错误请在框内打“×”,并写出你的解答过程.
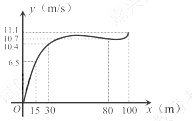
根据数学家凯勒的“百米赛跑数学模型”,前30米称为“加速期”,30米~80米为“中途期”.80米~100米为“冲刺期”.市田径队把运动员小斌某次百米跑训练时速度y (m/s)与路程x (m)之间的观测数据,绘制成曲线如图所示.
(1)y是关于x的函数吗?为什么?
(2)“加速期”结束时,小斌的速度为多少?
(3)根据右图提供的信息,给小斌提一条训练建议
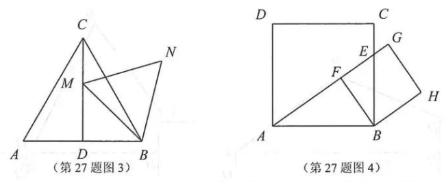
小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形ABCD绕点A顺时针旋转α( 0°<α≤90°),得到矩形AB"C'D',连结 BD.
【探究1】如图1,当α =90°时,点C'恰好在DB延长线上.若AB=1,求BC的长.
【探究2】如图2,连结AC',过点D'作 D'M// AC'交BD于点M.线段D'M与DM相等吗?请说明理由.
【探究3】在探究2的条件下,射线DB分别交AD',AC'于点P,N(如图3),发现线段DN,MN,PN存在一定的数量关系,请写出这个关系式,并加以证明.
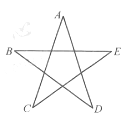
为庆祝中国共产党建党100周年,某校用红色灯带制作了一个如图所示的正五角星(A,B,C,D.E是正五边形的五个顶点),则图中二A的度数是__度
埃及胡夫金字塔是古代世界建筑奇迹之一,其底面是正方形,侧面是全等的等腰三角形底面正方形的边长与侧面等媵三角形底边上的高的比值是√5- 1,它介于整散n 和 n+1之间,则n的值是_
某快餐店销售A,B两种快餐,每份利润分别为12元,8元,每天卖出份数分别为40 份,80份.该店为了增加利润,准备降低每份A种快餐的利润,同时提高每份B种快餐的利润.售卖时发现,在一定范围内,每份A种快餐利润每降1元可多卖2份,每份B种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变,那么这两种快餐一天的总利润最多是_▲_元.
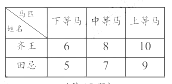
看了《田忌赛马》故事后,小杨用数学模型来分析:齐王与田忌的上中下三个等级的三匹马记分如右表,每匹马只赛一场,两数相比,大数为胜,三场两胜则赢.已知齐王的三匹马出场顺序为10,8,6.若田忌的三匹马随机出场,则田忌能赢得比赛的概率为_▲.