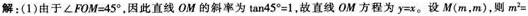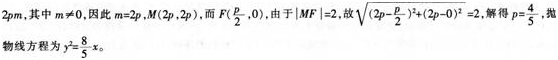- A (-1,-1)
- B (1,-1)
- C (1,1)
- D (-1,1)
- 参考答案:A
- 您的答案:
参考解析:

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
某篮球队12名队员的年龄如下表所示,则这12名队员年龄的众数和中位数分别是( )。

- A 2,19
- B 18,19
- C 2,19.5
- D 18,19.5
- 参考答案:B
- 您的答案:
参考解析:
众数是一组数据中出现次数最多的数值,本题中是18;当数据个数N为奇数时,处于中间位置的数值即为中位数;当N为偶数时,中位数则为处于中间位置的2个数的平均数,本题中N=12,中位数为19。
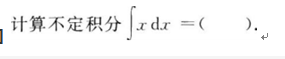

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:
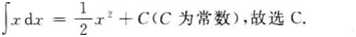

?k的值是().
?
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:A
- 您的答案:
参考解析:
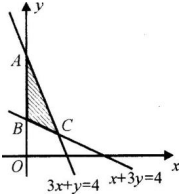
不等式组表示的平面区域如右图中阴影部分,三个交点的坐标

已知集合M={x|-3<x≤5),N={x}-5
- A {x{-5<x<5}
- B {x{-3<x<5)
- C (x|-5<x≤5}
- D {x|-3<x≤5)
- 参考答案:B
- 您的答案:
参考解析:
通过画数轴.即可确定选项B正确。
一个等差数列首项为32,该数列从第15项开始小于1,则此数列的公差d的取值范围是().?
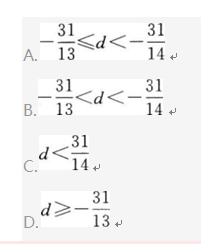
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:A
- 您的答案:
参考解析:
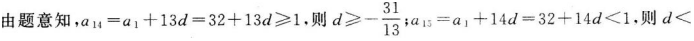
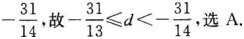


- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:

通过摆事实、讲道理,使学生提高认识、形成正确观点的德育方法是().?
- A 榜样法
- B 锻炼法
- C 说服法
- D 陶冶法
- 参考答案:C
- 您的答案:
参考解析:
榜样法是以他人的高尚思想、模范行为和卓越成就来影响学生品德的方法.锻炼法是有目的地组织学生进行一定的实际活动以培养他们的良好品德的方法.说服法是通过摆事实、讲道理,使学生提高认识、形成正确观点的方法.陶冶法是通过创设良好的情景,潜移默化地培养学生品德的方法.
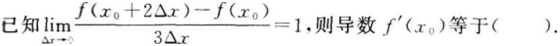

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
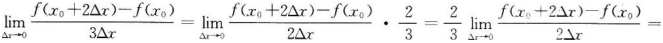
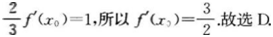
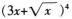
的展开式中x3的系数是( )。
- A 12
- B 27
- C 36
- D 54
- 参考答案:D
- 您的答案:
参考解析:
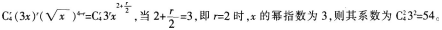
从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为().

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
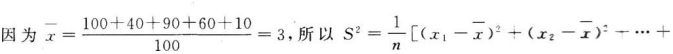
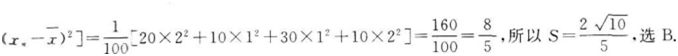
班主任既通过对集体的管理去间接影响个人,又通过对个人的直接管理去影响集体,从而把对集体和个人的管理结合起来的管理方式是().
- A 常规管理
- B 平行管理
- C 民主管理
- D 目标管理
- 参考答案:B
- 您的答案:
参考解析:
班级平行管理是指班主任既通过对集体的管理去间接影响个人,又通过对个人的直接管理去影响集体,从而把对集体和个人的管理结合起来的管理方式.
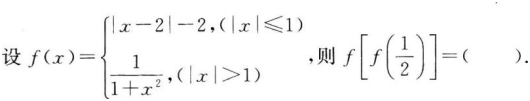
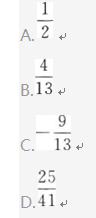
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:A
- 您的答案:
参考解析:
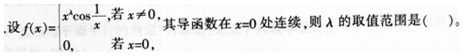
- A λ>2
- B λ<2
- C λ>12
- D λ≤2
- 参考答案:A
- 您的答案:
参考解析:

不同的五种商品在货架上排成一排,其中甲、乙两种必须排在一起,丙、丁两种不能排在一起,则不同的排法种数共有( ).
- A 12种
- B 20种
- C 24种
- D 48种
- 参考答案:C
- 您的答案:
参考解析:
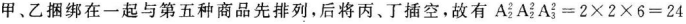
(种).选C.
在等差数列{an}中,a1+a5+a9=2π,则tan(a2+a8)值为( )。
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
由等差数列性质得
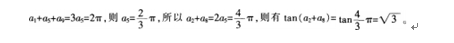
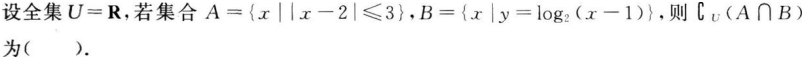
- A {x|1<x≤5}
- B {x|x≤-1或x>5}
- C {x|x≤1或x>5}
- D {x|-1≤x≤5}
- 参考答案:C
- 您的答案:
参考解析:
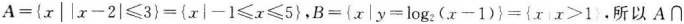

关于二次函数y=2-(x+1)2的图象,下列说法正确的是( )。
- A 图象开口向上
- B 图象的对称轴为直线x=1
- C 图象有最低点
- D 图象的顶点坐标(-1,2)
- 参考答案:D
- 您的答案:
参考解析:
由二次函数图象的性质可知,其开口方向向下,有最大值2,对称轴为x=-1,顶点坐标(-1,2)。二次函数y=a(x+h)2+k(α≠0)中,α决定了二次函数图象的开口方向,顶点坐标为(-h,k)。
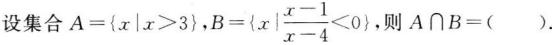
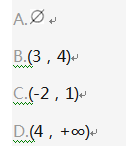
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:

玻璃杯成箱出售,每箱20只,假设各箱含0、1、2只残次品的概率分别为0.8、0.1和0.095。一顾客欲购一箱玻璃杯,在购买时,售货员随意取一箱,顾客开箱随机地察看四只,若无残次品.则买下该箱玻璃杯,否则退回,试求:
(1)顾客买下该箱玻璃杯的概率p;
(2)在顾客买下的一箱中,确实没有残次品的概率q。
- 参考答案:
- 您的答案:
参考解析:

- 参考答案:
- 您的答案:
参考解析:
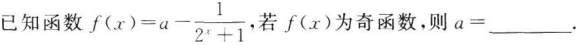
- 参考答案:
- 您的答案:
参考解析:

某班有50名学生,其中15人选修A课程,另外35人选修B课程,从班级中任选两名学生,他们是选修不同课程的学生的概率是_________.
- 参考答案:
- 您的答案:
参考解析:
50名学生中每个学生被取到的可能性是均等的,是等可能事件,由题干知.所求概率为P
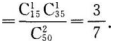

- 参考答案:
- 您的答案:
参考解析:
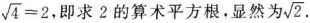
若p为非负实数,随机变量ξ的概率分布为

则Eξ的最大值为__________,Dξ最大值为__________.
- 参考答案:
- 您的答案:
参考解析:
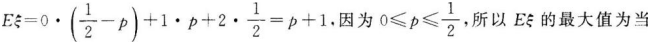
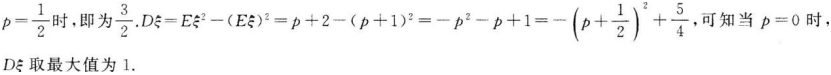
已知对称轴为坐标轴的双曲线有一条渐近线的方程为2x-y=0,则双曲线的离心率为
- 参考答案:
- 您的答案:
参考解析:


若角120°的终边上有一点(-4,a),则a的值为 ___________.
- 参考答案:
- 您的答案:
参考解析:
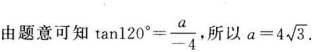
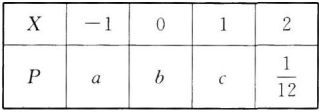
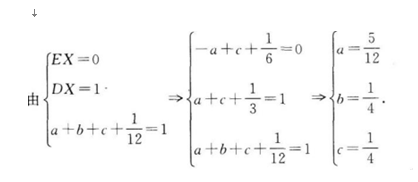
已知离散型随机变量X的分布列如下表.若EX=0,DX=1,则a=__________,b=__________.
- 参考答案:
- 您的答案:
参考解析:
用三种不同颜色给3个矩形随机涂色,每个矩形上涂一种颜色,则3个矩形颜色都不同的概率是 _________ .
- 参考答案:
- 您的答案:
参考解析:

用描述法表示图中阴影部分的点(包括边界上的点)的坐标的集合应为__________.
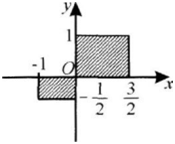
- 参考答案:
- 您的答案:
参考解析:
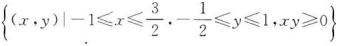
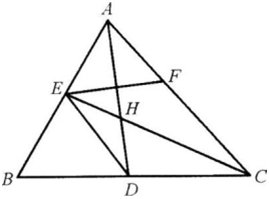
如图,已知△ABC的两条角平分线AD和CE相交于H,∠B=60。,F在AC上,且AE=AF.
(1)证明:B,D,H,E四点共圆;
(2)证明:CE平分∠DEF.
- 参考答案:
- 您的答案:
参考解析:
证明:(1)在△ABC中,因为∠B=60°,
所以∠BAC+∠BCA=120°.
因为AD,CE是角平分线.
所以∠HAC+∠HCA=60°,故∠AHC=120°.
于是∠EHD=∠AHC=120°.
因为∠EBD+∠EHD=180°.所以B,D,H,E四点共圆.
(2)连接BH,则BH为∠ABC的平分线,得∠HBD=30°,
由(1)知B,D,H,E四点共圆,所以∠CED=∠HBD=30°.
又∠AHE=∠EBD=60°,由已知AE=AF,AD平分∠EAF,
可得EF⊥AD,所以∠CEF=30°.所以CE平分∠DEF.
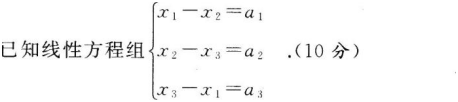
(1)讨论常数a1,a2,a3满足什么条件时,方程组有解.
(2)当方程组有无穷多解时,求出其通解(要求用它的一个特解和导出组的基础解系表示).
- 参考答案:
- 您的答案:
参考解析:
解:(1)将其增广矩阵化为简化行阶梯形矩阵T

“五一”假期期间,某学校计划组织385名师生租车旅游,现知道租车公司有42座和60座两种客车,42座客车的租金每辆为320元,60座客车的租金每辆为460元.
(1)若学校只租用42座客车或者只租用60座客车,那么学校各需多少租金?
(2)若学校同时租用这两种客车共8辆(可以坐不满),而且要比单独只租用一种车辆节省租金.请你帮助该学校选择一种最节省的租车方案.
- 参考答案:
- 您的答案:
参考解析:
解:(1)385÷42≈9.2,所以单独租用42座客车需10辆,租金为320×10=3200(元).385÷60≈6.4,所以单独租用60座客车需7辆,租金为460×7=3220(元).
(2)设租用42座客车x辆,则60座客车(8-x)辆,由题意得,
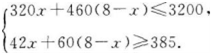
解得3.4≤x≤5.3.
由于x取整数,所以x=4或5.
当x=4时,租金为320×4+460×(8-4)=3120(元);
当x=5时,租金为320×5+460×(8-5)=2980(元).
故租用42座客车5辆,60座客车3辆,租金最少.
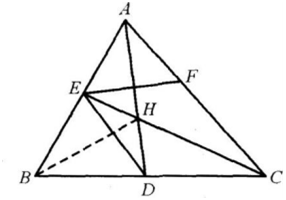
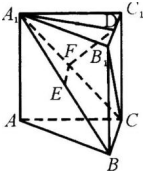
如图,在直三棱柱ABC—A1B1C1中,E,F分别是A1B,A1C的中点,点D在B1C,上,A1D⊥B1C,求证:(8分)
(1)EF∥平面ABC;
(2)平面A1FD上平面BB1C1C.
- 参考答案:
- 您的答案:
参考解析:
证明:(1)由E,F分别是A1B1A1C的中点知,EF∥BC,

已知M是抛物线y2=2px(p>0)上的点,F是抛物线的焦点,∠FOM=45o,|MF|=2。
(1)求抛物线的方程式;
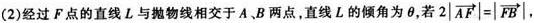
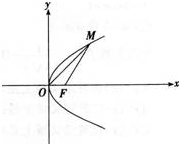
- 参考答案:
- 您的答案:
参考解析: