一堆钢管,最上层有5根,最下层有21根,如果自然堆码。这堆钢管最多能堆( )根.
- A 208
- B 221
- C 416
- D 442
- 参考答案:B
- 您的答案:
参考解析:
如果是自然堆码,最多的情况是:每相邻的下一层比它的上一层多1根,即构成了以5为首项,1为公差的等差数列,故可知21为第17项,从而这堆钢管最多能堆(5+
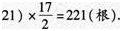
自然数中能被2整除的数都是( ).
- A 合数
- B 质数
- C 偶数
- D 奇数
- 参考答案:C
- 您的答案:
参考解析:
2能被2整除,但它是质数,故A错误;4能被2整除,但4是合数而不是质数,故B错误;奇数都不能被2整除,能被2整除的数都为偶数.
下列图形中,对称轴只有一条的是( ).
- A 长方形
- B 等边三角形
- C 等腰三角形
- D 圆
- 参考答案:C
- 您的答案:
参考解析:
长方形有两条对称轴,A排除.等边三角形有三条对称轴,B排除.圆有无数条对称轴,D排除.等腰三角形只有一条对称轴,即为底边上的中线(底边上的高或顶角平分线).
把5克食盐溶于75克水中,盐占盐水的( ).
- A 1/20
- B 1/16
- C 1/15
- D 1/14
- 参考答案:B
- 您的答案:
参考解析:
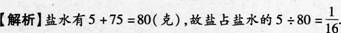
设三位数2a3加上326,得另一个三位数5b9,若5b9能被9整除,则a+b等于( ).
- A 2
- B 4
- C 6
- D 8
- 参考答案:C
- 您的答案:
参考解析:
由2a3+326=5b9可得,a+2=b,又5b9能被9整除,可知b=4,则a=2,所以a+b=2+4=6.
“棱柱的一个侧面是矩形”是“棱柱为直棱柱”的( ).
- A 充要条件
- B 充分但不必要条件
- C 必要但不充分条件
- D 既不充分又不必要条件
- 参考答案:C
- 您的答案:
参考解析:

有限小数的另一种表现形式是( ).
- A 十进分数
- B 分数
- C 真分数
- D 假分数
- 参考答案:A
- 您的答案:
参考解析:

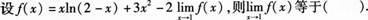
- A -2
- B 0
- C 1
- D 2
- 参考答案:C
- 您的答案:
参考解析:

如果曲线Y=f(x)在点(x,y)处的切线斜率与x2成正比,并且此曲线过点(1,-3)和(2,11),则此曲线方程为( ).
- A Y=3-2
- B Y=2x3-5
- C Y=x2-2
- D Y=2x2-5
- 参考答案:B
- 您的答案:
参考解析:
由曲线过点(1,-3)排除A、C项.由此曲线过点(2,11)排除D,故选B.Y=2x3-5显然过点(1,-3)和(2,11),且它在(x,Y)处的切线斜率为6x2,显然满足与x2成正比.
设A与B为互不相容事件,则下列等式正确的是( ).
- A P(AB)=1
- B P(AB)=0
- C P(AB)=P(A)P(B)
- D P(AB)=P(A)+P(B)
- 参考答案:B
- 您的答案:
参考解析:
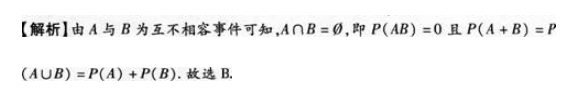
用0-9这十个数字组成最小的十位数是_______,四舍五入到万位,记作_______万.
- 参考答案:1023456789 102346
- 您的答案:
参考解析:
在一个边长为6厘米的正方形中剪一个最大的圆,它的周长是_______厘米;面积是_______.
- 参考答案:6π 9π平方厘米
- 您的答案:
参考解析:

- 参考答案:17 10
- 您的答案:
参考解析:
汽车站的1路车20分钟发一次车,5路车15分钟发一次车,两车于8:00同时发车后,再遇到同时发车至少再过_______。
- 参考答案:60分钟
- 您的答案:
参考解析:
有一类数,每一个数都能被11整除,并且各位数字之和是20,问这类数中,最小的数是_______.
- 参考答案:1199
- 您的答案:
参考解析:
在Y轴上的截距是1,且与x轴平行的直线方程是_______。
- 参考答案:Y=1
- 您的答案:
参考解析:

- 参考答案:-1
- 您的答案:
参考解析:
函数f(x)=x3在闭区间[-1,1]上的最大值为_______.
- 参考答案:1
- 您的答案:
参考解析:
脱式计算(能简算的要简算):[112+(349-115)÷117]÷0.8.
- 参考答案:
- 您的答案:
参考解析:
解:[112+(349-115)÷117]÷0.8 =(112+234÷117)÷0.8
=(112+2)÷0.8
=142.5.
前进小学六年级参加课外活动小组的人数占全年级总人数的48%,后来又有4人参加课外活动小组,这时参加课外活动的人数占全年级的52%,问还有多少人没有参加课外活动
- 参考答案:
- 您的答案:
参考解析:
解:设全年级总人数为x人,则 x·48%+4=52%x
解得:x=100
所以没有参加课外活动的人数为100×(1-52%)=48(人).

- 参考答案:
- 您的答案:
参考解析:
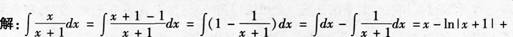
C(C为常数).
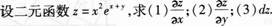
- 参考答案:
- 您的答案:
参考解析:
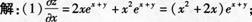
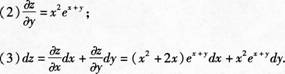
分析下题错误的原因,并提出相应预防措施。
“12能被0.4整除”
成因:
预防措施:
- 参考答案:
- 您的答案:
参考解析:
成因:没有理解整除的概念,对于数的整除是指如果一个整数a,除以一个自然数b,得到一个整数商C,而且没有余数,那么叫做a能被b整除或b能整除0,概念要求除数应为自然数,0.4是小数,而且混淆了整除与除尽两个概念,故错误。 预防措施:在讲整除概念时,应让学生清楚被除数、除数和商所要求数字满足的条件,即被除数应为整数,除数应为自然数,商应为整数.并且讲清整除与除尽的不同。
举一例子说明小学数学概念形成过程。
- 参考答案:
- 您的答案:
参考解析:
小学数学概念的形成过程主要包括:(1)概念的引入;(2)概念的形成;(3)概念的运用. 例如:对于“乘法分配律”的讲解:
(1)概念的引入:根据已经学过的乘法交换律,只是对于乘法的定律,在计算时,很多时候会遇到乘法和加法相结合的式子,如(21+14)×3.
(2)概念的形成:通过让学生计算,归纳发现乘法分配律.
比较大小①(32+11)×5=32×5+11×5
②(26+17)×2=26×2+17×2
学生通过计算后很容易发现每组中左右两个算式的结果相等,再引导学生观察分析,可以看出左边算式是两个数的和与一个数相乘,右边算式是两个加数分别与这个数相乘,再把两个积相加.虽然两个算式不同,但结果相同.然后就可以引导学生归纳总结出“乘法分配律”,即(a+b)×c=a×c+b×c.
(3)概念的运用:通过运用概念达到掌握此概念的目的.
计算下题:①(35+12)×10
②(25+12.5)×8
学生通过运用所学的乘法分配律会很快得到结果,比先算括号里两个数的和再乘外面的数要快的多,从而学生在以后的计算中会想到运用乘法分配律,也就掌握了概念。
下面是两位老师分别执教《接近整百、整千数加减法的简便计算》的片断,请你从数学思想方法的角度进行分析.
张老师在甲班执教:
1.做凑整(十、百)游戏;
2.抛出算式323+198和323-198,先让学生计算,再在小组内部交流,班内汇报讨论,讨论的问题是:把198看作什么数能使计算简便 加上(或减去)200后,接下去要怎么做 为什么 然后师生共同概括速算方法.……练习反馈表明,学生错误率相当高.主要问题是:在“323+198=323+200-2”中,原来是加法计算,为什么要减27在“323-198=323-200+2”中,原来是减法计算,为什么要加27
李老师执教乙班:给这类题目的速算方法找了一个合适的生活原型——生活实际中收付
钱款时常常发生的“付整找零”活动,以此展开教学活动.
1.创设情境:王阿姨到财务室领奖金,她口袋里原有124元人民币,这个月获奖金199元,现在她口袋里一共有多少元 让学生来表演发奖金:先给王阿姨2张100元钞(200元),王阿姨找还1元.还表演:小刚到商场购物,他钱包中有217元,买一双运动鞋要付198元,他给“营业员”2张100元钞,“营业员”找还他2元.
2.将上面发奖金的过程提炼为一道数学应用题:王阿姨原有124元,收入199元,现在共有多少元
3.把上面发奖金的过程用算式表示:124+199=124+200-1,算出结果并检验结果是否正确.
4.将上面买鞋的过程加工提炼成一道数学应用题:小刚原有217元,用了198元,现在还剩多少元 结合表演,列式计算并检验.
5.引导对比,小结整理,概括出速算的法则.……练习反馈表明,学生“知其然,也应知其所以然”.
- 参考答案:
- 您的答案:
参考解析:
分析建议:张教师主要用了抽象与概括的思想方法;李老师用了教学模型的方法,先从实际问题中抽象出数学模型,然后通过逻辑推理得出模型的解,最后用这-模型解决实际问题.教师可从这方面加以论述.
根据下面给出的例题,试分析其教学难点,并编写出突破难点的教学片段.
例:小明有5本故事书,小红的故事书是小明的2倍,小明和小红一共有多少本故事书
- 参考答案:
- 您的答案:
