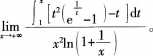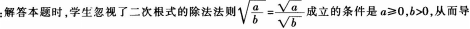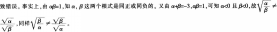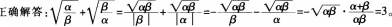《义务教育数学课程标准(2011年版)》提出,应当注重发展学生的数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力和( )
- A 探索性学习
- B 合作交流
- C 模型思想
- D 综合与实践
- 参考答案:C
- 您的答案:
参考解析:
在数学课程中,应该注重发展学生的数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力和模型思想。
已知线性方程组AX=Kβ1+β2有解,其中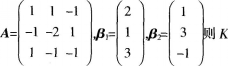
等于( )。
- A 1
- B -l
- C 2
- D -2
- 参考答案:D
- 您的答案:
参考解析:
已知线性方程组是非齐次的,如果方程要有解,则系数矩阵的秩要等于增广矩阵的秩.由此可以求出K。 
若函数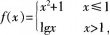
则f(10))=( )。
- A 19101
- B 2
- C 1
- D 0
- 参考答案:B
- 您的答案:
参考解析:
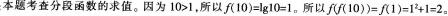
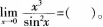
- A 0
- B 1
- C ∞
- D 2
- 参考答案:A
- 您的答案:
参考解析:
用洛必达法则即可求得。
设函数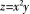
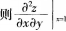 等于( )。
等于( )。
- A 1
- B 2
- C <img src='http://tp.mxqe.com/data/438/5386848_0_2.png' alt='中学数学学科知识与教学能力,章节练习,中学数学学科知识与教学能力预测' title='中学数学学科知识与教学能力,章节练习,中学数学学科知识与教学能力预测'>
- D <img src='http://tp.mxqe.com/data/438/5386848_0_3.png' alt='中学数学学科知识与教学能力,章节练习,中学数学学科知识与教学能力预测' title='中学数学学科知识与教学能力,章节练习,中学数学学科知识与教学能力预测'>
- 参考答案:B
- 您的答案:
参考解析:
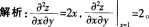
已知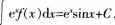 则f(x)ax:( )。
则f(x)ax:( )。
- A sinx+C
- B cosx+C
- C -cosx+sinx+C
- D cosx+sinx+C
- 参考答案:C
- 您的答案:
参考解析:
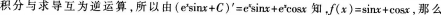
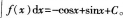
下列函数中,与函数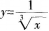 定义域相同的函数为( )。
定义域相同的函数为( )。
- A y=1/sinx
- B y=lnx/x
- C <img src='http://tp.mxqe.com/data/438/5386842_0_1.png' alt='中学数学学科知识与教学能力,章节练习,中学数学学科知识与教学能力预测' title='中学数学学科知识与教学能力,章节练习,中学数学学科知识与教学能力预测'>
- D y=sinx/x
- 参考答案:D
- 您的答案:
参考解析:
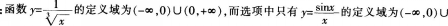

下列命题中,假命题为( )。
- A 存在四边相等的四边形不是正方形
- B z1,z2∈C,zl=z2为实数的充分必要条件是z1+z2互为共轭复数
- C 若X,Y∈R,且x+y>2,则X,Y至少有一个大于1
- D <img src='http://tp.mxqe.com/data/438/5386843_0.png' alt='中学数学学科知识与教学能力,章节练习,中学数学学科知识与教学能力预测' title='中学数学学科知识与教学能力,章节练习,中学数学学科知识与教学能力预测'>
- 参考答案:B
- 您的答案:
参考解析:
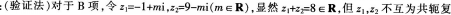 数,故B为假命题,应选B。
数,故B为假命题,应选B。
“三角形的中位线”是初中学习三角形知识点中必不可少的内容。对学生的要求是必须了解三角形中位线的概念,熟练掌握三角形中位线定理的证明和有关应用。
(1)该课程设定需要使学生达到什么能力目标
(2)本课程的教学重点与难点。
(3)教学过程(只要求写出新课导入和新知识探究、巩固、应用等)及设计意图。
- 参考答案:
- 您的答案:
参考解析:
(1)该课程设定需要使学生达到:
①经历“探索一发现一猜想一证明”的过程,进一步发展推理论证能力。
②能够用多种方法证明三角形的中位线定理,体会在证明过程中所运用的归纳、类比、转化等数学思想方法。
③能够应用三角形的中位线定理进行有关的论证和计算,逐步提高学生分析问题和解决问题的能力。
(2)教学重点与难点
教学重点:三角形中位线的概念与三角形中位线定理的证明。
教学难点:三角形中位线定理的多种证明。
(3)教学过程
①一道趣题——课堂因你而和谐
问题:你能将任意一个三角形分成四个全等的三角形吗 这四个全等三角形能拼凑成一个平行四边形吗 (板书)
(这一问题激发了学生的学习兴趣,学生积极主动地加入到课堂教学中,课堂气氛变得较为和谐,课堂也鲜活起来了。)
学生想出了这样的方法:顺次连接三角形每两边的中点,看上去就得到了四个全等的三角形。将AADE绕E点沿顺(逆)时针方向旋转l800可得平行四边形ADFE。
问题:你有办法验证吗
②一种实验——课堂因你而生动
学生的验证方法较多.其中较为典型的方法如下:生l:沿DE、DF、EF将画在纸上的AABC剪开,看四个三角形能否重合。生2:分别测量四个三角形的三边长度,判断是否可利用“SSS”来判定三角形全等。生3:分别测量四个三角形对应的边及角,判断是否可用“SAS、ASA或AAS”判定全等。
引导:上述同学都采用了实验法,存在误差,那么如何利用推理论证的方法验证呢
③一种探索——课堂因你而鲜活
师:把连接三角形两边中点的线段叫做三角形的中位线。(板书)
问题:三角形的中位线与第三边有怎样的关系呢 在前面图l中你能发现什么结论呢 (学生的思维开始活跃起来,同学之间开始互相讨论,积极发言)
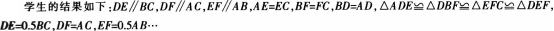
猜想:三角形的中位线平行于第三边,且等于第三边的一半。(板书)
师:如何证明这个猜想的命题呢
生:先将文字问题转化为几何问题然后证明。
已知:DE是ABC的中位线,求证:DE//BC、DE--0.5BC。学生思考后教师启发:要证明两条直线平行,可以利用。三线八角”的有关内容进行转化,而要证明一条线段的长等于另一条线段长度的一半,可采用将较短的线段延长一倍,或者截取较长线段的一半等方法进行转化归纳。(学生积极讨论,得出几种常用方法.大致思路如下)
生l:延长DE到F使EF=DE.连接CF

问题:三角形的中位线与中线有什么区别与联系呢
容易得出如下事实:都是三角形内部与边的中点有关的线段。但中位线平行于第三边,且等于第三边的一半,三角形的一条中位线与第三边上的中线互相平分。(学生交流、探索、思考、验证)
⑤一种照应——课堂因你而完整
问题:你能利用三角形中位线定理说明本节课开始提出的趣题的合理性吗 (学生争先恐后回答.课堂气氛活跃)
⑥一句总结——课堂因你而彰显无穷魅力
学生总结本节内容:三角形的中位线和三角形中位线定理。(另附作业)
⑦课后反思
本节课以“如何将一个任意三角形分为四个全等的三角形”这一问题为出发点,以平行四边形的性质定理和判定定理为桥梁,探究了三角形中位线的基本性质和应用。在本节课中,学生亲身经历了“探索一发现一猜想一证明”的探究过程,体会了证明的必要性和证明方法的多样性。在此过程中,笔者注重新旧知识的联系,同时强调转化、类比、归纳等数学思想方法的恰当应用,达到了预期的目的。
一商家销售某种商品的价格满足关系P=7—0.2x(万元/吨),其中x为销售量,该商品的成本函数为C=3x+l(万元)。
(1)若每销售一吨商品,政府要征税t万元,求该商家获最大利润时的销售量;
(2)t为何值时,政府税收总额最大
探究学习应该注意的问题
- 参考答案:
- 您的答案:
参考解析:
(1)面向全体学生,并关照个别差异。(2)注重为学生提供相关的支持条件。(3)注重发挥教师自身的指导作用。(4)要注重分析探究中学生独特的感受、体验和理解。(5)要强调学生之间的合作与交流。(6)引导学生关注探究的连续性和艰巨性。
怎么认识数学
- 参考答案:
- 您的答案:
参考解析:
《义务教育数学课程标准(2011年版)》(以下简称《标准》)指出,数学是人类生活的工具;数学是人类用于交流的语言;数学能赋予人创造性;数学是一种人类文化。《标准》对数学没有采取简单定义的方法。因为数学不仅是一门知识,更是人类实践活动创造的产物,是由诸多元素构成的多元结构;社会与文化不仅推动着数学的发展.同时数学对推动社会与文化发展也起关键的作用;对数学的认识不仅要从数学家关于数学本质的观点中领悟.更要从数学活动的亲身实践中去体验。从课堂教学的眼光看待数学:大众数学、生活数学、活动数学、探索数学。
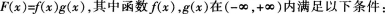
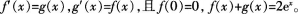 (1)求F(x)所满足的一阶微分方程;
(1)求F(x)所满足的一阶微分方程;
(2)求出F(x)的表达式。
- 参考答案:
- 您的答案:
参考解析:
题目要求F(x)所满足的微分方程,而微分方程中含有其导函数,自然想到对F(x)求导,并将其余部分转化为用F(x)表示,导出相应的微分方程,然后再求解相应的微分方程即可。
(1)
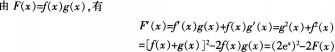
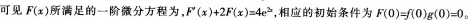
(2)由题(1)得到F(x)所满足的一阶微分方程,求,(x)的表达式只需解一阶微分方程。又一阶线性非齐次

函数知识一直是中学代数内容的主线。是研究代数、三角函数、数列、方程和不等式等初等数学内容的基础,函数思想又是数学解题中的重要思想,这就决定了函数在中学数学中的重要地位。
请说明初中函数内容教学的要求,并结合自己的教学,谈谈利用函数思想解决问题时,重点要注意的问题是什么 并举出两个你印象最为深刻的利用函数思想解题的例子。
- 参考答案:
- 您的答案:
参考解析:
初中函数的要求:①能探索具体问题中的数量关系和变化规律;②了解常量、变量的意义,了解函数概念和表示方法;③能结合图象分析,能用适当函数表示刻画某些实际问题中变量之间的关系;④对具体的一次函数、二次函数、反比例函数体会意义,画出图象,确定解析式、能利用函数解决一些实际问题。
利用函数思想解决问题时要注意的问题是:①函数知识的横向、纵向联系;②把函数、方程、不等式看成一个整体:③将函数性质、特征与图象紧密结合;④二次函数的综合运用;⑤实际问题通过建立函数模型解决等。
案例:某教师在进行二次根式教学时,给学生出了如下一道练习题: 已知方程x2+3x+1=0的两个根分别为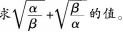 ,α,β 某学生的解答过程如下:
,α,β 某学生的解答过程如下: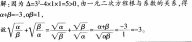 问题: (1)指出该生解题过程中的错误,分析其错误原因; (2)给出你的正确解答; (3)指出你解题所运用的数学思想方法。
问题: (1)指出该生解题过程中的错误,分析其错误原因; (2)给出你的正确解答; (3)指出你解题所运用的数学思想方法。