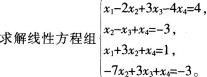数学史上一共发生了几次危机 ( )
- A 1
- B 2
- C 3
- D 4
- 参考答案:C
- 您的答案:
参考解析:
一共发生了三次,分别是:无理数的发现,无穷小是零吗,罗素悖论的产生。
设A是m×n矩阵,如果m<n,则( )。
- A Ax=b必有无穷多解
- B Ax=b必有唯一解
- C Ax=0必有非零解
- D Ax=0必有唯一解
- 参考答案:C
- 您的答案:
参考解析:
根据条件可知,方程组中方程的个数一定小于未知数的个数,所以Ax=0必有非零解。由
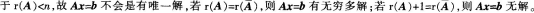

- A 如上图所示
- B 如上图所示
- C 如上图所示
- D 如上图所示
- 参考答案:D
- 您的答案:
参考解析:
线性方程组Ax=b有无穷多解的充分必要条件为:r(A)=r(A,b)<3。
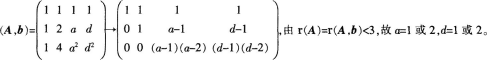
古希腊的三大著名几何尺规作图问题是()。
①三等分角②立方倍积③正十七边形④化圆为方
- A ①②③
- B ①②④
- C ①③④
- D ②③④
- 参考答案:B
- 您的答案:
参考解析:
大约在公元前6世纪至公元前4世纪之间,古希腊人遇到了令他们百思不得其解的三大尺规作图问题,这就是著名的古代几何作图三大难题:(1)三等分角问题:将任一个给定的角三等分;(2)立方倍积问题:求作一个正方体的棱长,使这个正方体的体积是已知正方体体积的二倍;(3)化圆为方问题:求作一个正方形。使它的面积和已知圆的面积相等。
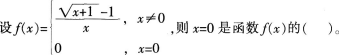
- A 可去间断点
- B 无穷间断点
- C 连续点
- D 跳跃间断点
- 参考答案:A
- 您的答案:
参考解析:
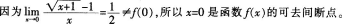
设λ1,λ2是矩阵A的两个不同的特征值,对应的特征向量分别为a1,a2,则a1,A(a1+a2)线性无关的充分必要条件是( )。
- A λ1=0
- B λ2=0
- C λ1≠0
- D λ2≠0
- 参考答案:D
- 您的答案:
参考解析:

我国古代关于求解一次同余式组的方法被西方称作“中国剩余定理”,这一方法的首创者是()。
- A 贾宪
- B 刘徽
- C 朱世杰
- D 秦九韶
- 参考答案:D
- 您的答案:
参考解析:
秦九韶(约1202-1261),所著《数书九章》是一部划时代的巨著,它完整保存了中国算筹记数法及其演算式,论述了自然数、分数、小数、复数,还第一次用小数表示无理根。《数书九章》还对“大衍求一术”(一次同余组解法)和“正负开方术”(高次方程的数值解法)等进行了十分深入的研究。
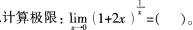
- A 0
- B 1
- C e
- D e2
- 参考答案:D
- 您的答案:
参考解析:
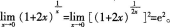
简述创造性思维的特点,在数学教学中如何培养学生的创造性。
- 参考答案:
- 您的答案:
参考解析:
创造性思维具有如下五个重要特点:
①新颖、独特且有意义的思维活动;
②思维加想象是创造性思维的两个重要成分;
③在创造性思维过程中,新形象和新假设的产生有突然性,常被称为“灵感”;
④分析思维和直觉思维的统一;
⑤创造性思维是发散思维与辐合思维的统一。
在数学教学中培养创造性思维:(1)培养归纳、类比能力,鼓励大胆猜想;(2)一题多解,培养发散思维能力:(3)鼓励质疑提问,培养思维的批判性;(4)重视直觉思维能力培养;(5)引入数学开放题;(6)指导学生写数学小论文;(7)多一点耐心和宽容。
分别解释学习心理学中“同化”与“顺应”的含义,并举例说明“同化”在数学概念学习中的作用。
- 参考答案:
- 您的答案:
参考解析:
同化是指有机体面对一个新的刺激情景时,把刺激整合到已有的图式或认知结构中。顺应是指当有机体不能利用原有图式接受和解释新刺激时,其认知结构发生改变来适应刺激的影响。同化论,强调新旧知识的相互作用涉及上位学习、下位学习、并列结合学习三种形式:强调概念和命题的不断分化和综合贯通;强调原有知识的巩固及教材由一般到个别的循序组织。实际应用中,要了解学生对新旧知识的掌握程度及接受能力,用耳熟能详的“已知”内容去教导“未知”内容。比如我们在学习椭圆的时候,可以从“圆”类比着来学习。
数感是《义务教育数学课程标准(2011年版)》提到的课程核心之一,学生的数感主要表现在哪些方面
- 参考答案:
- 您的答案:
参考解析:
理解数的意义;能用多种方法来表示数;能在具体的情境中把握数的相对大小关系;能用数来表达和交流信息;能为解决问题而选择恰当的算法;能估计运算的结果,并对结果的合理性做出解释。
试分别叙述罗尔中值定理和拉格朗日中值定理。若以S(x)记由(a,(a)),(b,(b)),(x,(x)))三点组成的三角形面积,试对S(x)应用罗尔中值定理证明拉格朗日中值定理。
- 参考答案:
- 您的答案:
参考解析:
罗尔中值定理:若函数(x)满足如下条件: (1)(x)在闭区间[a,b]上连续;
(2)(x)在开区间(a,b)内可导;
(3)(a)=(b),
则在(a,b)内至少存在一点ξ,使得’(ξ)=0。
拉格朗日中值定理:若函数(x)满足如下条件:
(1)(x)在闭区间[a,b]上连续;
(2)(x)在开区间(a,b)内可导,
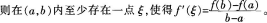
在xOy面上考虑,记由A(a,(a),0),B(b,(b),0),C(x,(x),0)三点组成的三角形面积S(x),则

什么是空间观念举例说明(初中内容)在教学中应该怎样培养学生的空间想象能力
- 参考答案:
- 您的答案:
参考解析:
空间观念主要是指根据物体特征抽象出几何图形,根据几何图形想象出所描述的实际物体:想象出物体的方位和相互之间的位置关系;描述图形的运动和变化;依据语言的描述画出图形等。 (1)让学生学好有关反映空间观念的课程内容和有关空间形式的数学基础知识:如三角形、平行四边形的概念性质等等;
(2)从学生的认识规律人手,通过实物或模型的观察、解剖、分析、制作等实践活动,形成学生的空间观念。如平行四边形的判定,先做一个模型得到结论再利用定义和已学习过的去证明:
(3)培养学生看图能力,教给学生正确的画图规律和方法,是培养学生的观察力和空间想象能力的主要途径之一;如对称图形的画法、全等的画法:
(4)通过平面图形折叠的教学培养学生的空间想象能力:
(5)通过变式教学强化空间观念;
(6)通过对多面体和旋转体的侧面展开、组合、切割、运动来提高学生的空间想象能力;
(7)加强对几何体截面的教学,提高空间想象能力。

问题:(1)该同学的解题过程哪步错了分析原因;
(2)针对该生的情况,请你设计一个辅导教学片段,并说明设计意图;
(3)怎样防范这样的错误呢
- 参考答案:
- 您的答案:
参考解析:
(1)该同学没有考虑x<0的情形; (2)教学片段:
师:我们知道函数是有定义域的,那么函数y=2/x的定义域是什么
生:x大于0或x小于0。
师:是的,那么同学可以画出它的图像吗大家试试。
师:当x≤3时y的取值范围是什么呢
师:是不是还要考虑x小于0的情形呢
生:是……
师:那么当x≤3时Y的取值范围是什么呢
生:y≥2/3或y<0
师:很好,大家以后解题时一定不要急于求成,而要认真地思考。
设计意图:让学生在解关于函数的题型时首先要考虑函数的定义域,在定义域上研究函数。
(3)防范这种错误的方法是结合图像,注意反比例函数的图像是两支,在每一个象限内的情形要分开来解决。
“三角形的中位线”是初中学习三角形知识点中必不可少的内容。对学生的要求是必须了解三角形中位线的概念,熟练掌握三角形中位线定理的证明和有关应用。
(1)该课程设定需要使学生达到什么能力目标
(2)本课程的教学重点与难点。
(3)教学过程(只要求写出新课导入和新知识探究、巩固、应用等)及设计意图。
- 参考答案:
- 您的答案:
参考解析:
(1)该课程设定需要使学生达到:
①经历“探索一发现一猜想一证明”的过程,进一步发展推理论证能力。
②能够用多种方法证明三角形的中位线定理,体会在证明过程中所运用的归纳、类比、转化等数学思想方法。
③能够应用三角形的中位线定理进行有关的论证和计算,逐步提高学生分析问题和解决问题的能力。
(2)教学重点与难点
教学重点:三角形中位线的概念与三角形中位线定理的证明。
教学难点:三角形中位线定理的多种证明。
(3)教学过程
①一道趣题——课堂因你而和谐
问题:你能将任意一个三角形分成四个全等的三角形吗 这四个全等三角形能拼凑成一个平行四边形吗 (板书)
(这一问题激发了学生的学习兴趣,学生积极主动地加入到课堂教学中,课堂气氛变得较为和谐,课堂也鲜活起来了。)
学生想出了这样的方法:顺次连接三角形每两边的中点,看上去就得到了四个全等的三角形。将AADE绕E点沿顺(逆)时针方向旋转l800可得平行四边形ADFE。
问题:你有办法验证吗
②一种实验——课堂因你而生动
学生的验证方法较多.其中较为典型的方法如下:生l:沿DE、DF、EF将画在纸上的AABC剪开,看四个三角形能否重合。生2:分别测量四个三角形的三边长度,判断是否可利用“SSS”来判定三角形全等。生3:分别测量四个三角形对应的边及角,判断是否可用“SAS、ASA或AAS”判定全等。
引导:上述同学都采用了实验法,存在误差,那么如何利用推理论证的方法验证呢
③一种探索——课堂因你而鲜活
师:把连接三角形两边中点的线段叫做三角形的中位线。(板书)
问题:三角形的中位线与第三边有怎样的关系呢 在前面图l中你能发现什么结论呢 (学生的思维开始活跃起来,同学之间开始互相讨论,积极发言)
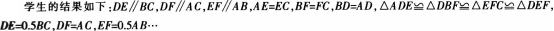
猜想:三角形的中位线平行于第三边,且等于第三边的一半。(板书)
师:如何证明这个猜想的命题呢
生:先将文字问题转化为几何问题然后证明。
已知:DE是ABC的中位线,求证:DE//BC、DE--0.5BC。学生思考后教师启发:要证明两条直线平行,可以利用。三线八角”的有关内容进行转化,而要证明一条线段的长等于另一条线段长度的一半,可采用将较短的线段延长一倍,或者截取较长线段的一半等方法进行转化归纳。(学生积极讨论,得出几种常用方法.大致思路如下)
生l:延长DE到F使EF=DE.连接CF

问题:三角形的中位线与中线有什么区别与联系呢
容易得出如下事实:都是三角形内部与边的中点有关的线段。但中位线平行于第三边,且等于第三边的一半,三角形的一条中位线与第三边上的中线互相平分。(学生交流、探索、思考、验证)
⑤一种照应——课堂因你而完整
问题:你能利用三角形中位线定理说明本节课开始提出的趣题的合理性吗 (学生争先恐后回答.课堂气氛活跃)
⑥一句总结——课堂因你而彰显无穷魅力
学生总结本节内容:三角形的中位线和三角形中位线定理。(另附作业)
⑦课后反思
本节课以“如何将一个任意三角形分为四个全等的三角形”这一问题为出发点,以平行四边形的性质定理和判定定理为桥梁,探究了三角形中位线的基本性质和应用。在本节课中,学生亲身经历了“探索一发现一猜想一证明”的探究过程,体会了证明的必要性和证明方法的多样性。在此过程中,笔者注重新旧知识的联系,同时强调转化、类比、归纳等数学思想方法的恰当应用,达到了预期的目的。